Exam 4: Applications of Differentiation
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find by evaluating the integral using Part 2 of the Fundamental Theorem and then differentiating.
(Short Answer)
4.8/5  (44)
(44)
The velocity graph of a car accelerating from rest to a speed of over a period of 10 seconds is shown. Estimate to the nearest integer the distance traveled during this period. Use a right sum with .
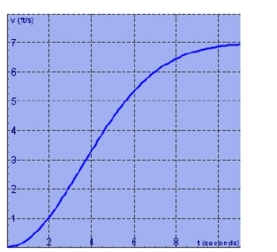
(Short Answer)
4.8/5  (40)
(40)
If is a child's rate of growth in pounds per year, which of the following expressions represents the increase in the child's weight (in pounds) between the years 3 and 7 ?
(Multiple Choice)
4.9/5  (35)
(35)
Find the integral using the indicated substitution.
Select the correct answer.
(Multiple Choice)
4.8/5  (39)
(39)
Find the area of the region that lies under the given curve. Round the answer to three decimal places.
Select the correct answer.
(Multiple Choice)
4.8/5  (38)
(38)
Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function.
Select the correct answer.
(Multiple Choice)
4.9/5  (33)
(33)
Find the area of the region under the graph of on .
Select the correct answer.
(Multiple Choice)
4.8/5  (28)
(28)
Use the Midpoint Rule with to approximate the integral. Round the answer to 3 decimal places.
(Short Answer)
4.7/5  (41)
(41)
Use Part 1 of the Fundamental Theorem of Calculus to find the derivative of the function.
(Short Answer)
4.8/5  (37)
(37)
Showing 41 - 60 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)