Exam 14: Partial Derivatives
Exam 1: Functions and Models179 Questions
Exam 2: Limits and Derivatives139 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation160 Questions
Exam 5: Integrals158 Questions
Exam 6: Applications of Integration157 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series159 Questions
Exam 12: Vectors and the Geometry of Space160 Questions
Exam 13: Vector Functions159 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals159 Questions
Exam 16: Vector Calculus159 Questions
Exam 17: Second-Order Differential Equations159 Questions
Select questions type
Find the directional derivative of at the point in the direction toward the point .
Select the correct answer.
(Multiple Choice)
4.8/5  (39)
(39)
Find three positive numbers whose sum is 291 and whose product is a maximum.
(Multiple Choice)
4.9/5  (38)
(38)
A contour map for a function is shown. Use it to estimate the value of .
Select the correct answer.
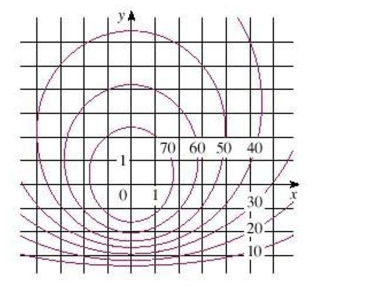
(Multiple Choice)
4.9/5  (31)
(31)
Use the definition of partial derivatives as limits to find if .
Select the correct answer.
(Multiple Choice)
4.8/5  (35)
(35)
A boundary stripe 2 in. wide is painted around a rectangle whose dimensions are by . Use differentials to approximate the number of square feet of paint in the stripe.
(Multiple Choice)
4.7/5  (40)
(40)
Suppose that over a certain region of space the electrical potential is given by
Find the rate of change of the potential at in the direction of the vector .
Select the correct answer.
(Multiple Choice)
4.9/5  (36)
(36)
Find the directional derivative of the function at the point in the direction of the unit vector that makes the angle with the positive -axis.
(Multiple Choice)
4.8/5  (35)
(35)
Showing 41 - 60 of 158
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)