Exam 2: Functions and Graphs
Exam 1: Equations, Inequalities, and Modeling531 Questions
Exam 2: Functions and Graphs365 Questions
Exam 3: Polynomial and Rational Functions396 Questions
Exam 4: Exponential and Logarithmic Functions203 Questions
Exam 5: The Trigonometric Functions398 Questions
Exam 6: Trigonometric Identities and Conditional Equations674 Questions
Exam 7: Applications of Trigonometry332 Questions
Exam 8: Systems of Equations and Inequalities293 Questions
Exam 9: Matrices and Determinants218 Questions
Exam 10: The Conic Sections218 Questions
Exam 11: Sequences, Series, and Probability338 Questions
Exam 12: Basic Algebra Review226 Questions
Select questions type
Find the specified domain.
-For f(x) = 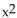 - 49 and g(x) = 2x + 3, what is the domain of f/g?
- 49 and g(x) = 2x + 3, what is the domain of f/g?
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-At Allied Electronics, production has begun on the X-15 Computer Chip. The total revenue function is given by R(x) = 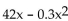 and the total profit function is given by P(x) =
and the total profit function is given by P(x) = 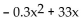 - 12, where x represents the
Number of boxes of computer chips produced. The total cost function, C(x), is such that C(x) = R(x) - P(x). Find
C(x).
- 12, where x represents the
Number of boxes of computer chips produced. The total cost function, C(x), is such that C(x) = R(x) - P(x). Find
C(x).
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-The shadow cast by an object on a sunny day varies directly as the height of the object. If a person 58 inches tall casts a shadow 84 inches long, how tall is a tree which casts a shadow 44 feet in length? Round to the nearest
Hundredth when necessary.
(Multiple Choice)
4.9/5  (29)
(29)
Solve the problem.
-Suppose the sales of a particular brand of appliance satisfy the relationship S(x) = 60x + 3300, where S(x) represents the number of sales in year x, with x = 0 corresponding to 1982. In what year would the sales be
3720?
(Multiple Choice)
4.9/5  (31)
(31)
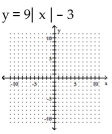
Graph the equation by plotting ordered pairs of numbers.
-
(Multiple Choice)
4.9/5  (35)
(35)
Determine whether the function is invertible by inspecting its graph on a graphing calculator.
-f(x) = 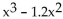 + 0.48x - 3
+ 0.48x - 3
(Multiple Choice)
4.8/5  (36)
(36)
Find the requested function value.
-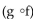 (x): f(x) =
(x): f(x) = 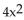 + 3x + 8, g(x) = 3x - 4
+ 3x + 8, g(x) = 3x - 4
(Multiple Choice)
4.8/5  (41)
(41)
Decide whether or not the functions are inverses of each other.
-f(x) = 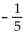 x, g(x) = - 5x
x, g(x) = - 5x
(Multiple Choice)
4.9/5  (39)
(39)
Graph the following function by transforming the given graph of y = f(x).
-Sketch the graph of y = f(x - 3). 
(Multiple Choice)
4.8/5  (23)
(23)
List the symmetries of the given function, if there are any. Otherwise, state "No symmetry".
-f(x) = 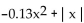 + 2
+ 2
(Multiple Choice)
4.8/5  (35)
(35)
Determine whether the function is even, odd, or neither.
-f(x) = (x + 9)(x + 9)
(Multiple Choice)
4.9/5  (29)
(29)
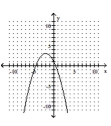
Use the vertical line test to determine whether y is a function of x.
-
(Multiple Choice)
4.9/5  (29)
(29)
Determine whether the relation is a function.
-{(-8, 8), (-8, 9), (-1, 6), (6, -1), (8, -9)}
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-The function 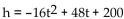 gives the height h, in feet, of a coin tossed upward from a balcony 200 ft high with an initial velocity of 48 ft/sec. During what interval of time will the coin be at a height of at least 40 ft?
gives the height h, in feet, of a coin tossed upward from a balcony 200 ft high with an initial velocity of 48 ft/sec. During what interval of time will the coin be at a height of at least 40 ft?
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-The volume V of a given mass of gas varies directly as the temperature T and inversely as the pressure P. If 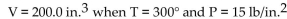 , what is the volume when T =
, what is the volume when T = 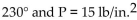
(Multiple Choice)
4.8/5  (33)
(33)
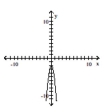
Determine the intervals on which the function is increasing, decreasing, and constant.
-
(Multiple Choice)
4.7/5  (31)
(31)
Showing 241 - 260 of 365
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)