Exam 2: Functions and Graphs
Exam 1: Equations, Inequalities, and Modeling531 Questions
Exam 2: Functions and Graphs365 Questions
Exam 3: Polynomial and Rational Functions396 Questions
Exam 4: Exponential and Logarithmic Functions203 Questions
Exam 5: The Trigonometric Functions398 Questions
Exam 6: Trigonometric Identities and Conditional Equations674 Questions
Exam 7: Applications of Trigonometry332 Questions
Exam 8: Systems of Equations and Inequalities293 Questions
Exam 9: Matrices and Determinants218 Questions
Exam 10: The Conic Sections218 Questions
Exam 11: Sequences, Series, and Probability338 Questions
Exam 12: Basic Algebra Review226 Questions
Select questions type
Graph the function as a solid curve and its inverse as a dashed curve.
-f(x) = 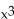 + 4
+ 4 
(Multiple Choice)
4.8/5  (30)
(30)
For the pair of functions, perform the indicated operation.
-f(x) = 4x - 3, g(x) = 7x - 9 Find f - g.
(Multiple Choice)
4.8/5  (35)
(35)
Solve the inequality by reading the given graph. State the solution set using interval notation.
-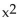 + 4x < 2x + 8 A related function is graphed below.
+ 4x < 2x + 8 A related function is graphed below. 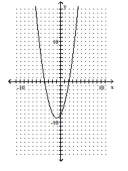 x-intercepts: (-4, 0), (2, 0)
x-intercepts: (-4, 0), (2, 0)
(Multiple Choice)
4.8/5  (24)
(24)
Find the constant of variation and construct the function that is expressed in each statement.
-y varies directly as x: y = 1.4, when x = 0.5
(Multiple Choice)
4.9/5  (31)
(31)
Find the requested composition of functions.
-Given f(x) = 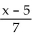 and g(x) = 7x + 5, find
and g(x) = 7x + 5, find 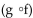 x).
x).
(Multiple Choice)
4.7/5  (26)
(26)
Solve the problem.
-A rectangular box with volume 188 cubic feet is built with a square base and top. The cost is $1.50 per square foot for the top and the bottom and $2.00 per square foot for the sides. Let x represent the length of a side of the
Base. Express the cost of the box as a function of x. Give the function and state its domain.
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the first variable varies directly or inversely with the other variable.
-The time it takes an athlete to run 100 meters, her average speed
(Multiple Choice)
4.8/5  (37)
(37)
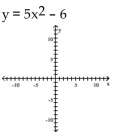
Use transformations to graph the function and state the domain and range.
-
(Multiple Choice)
4.8/5  (27)
(27)
Use transformations to graph the function and state the domain and range.
-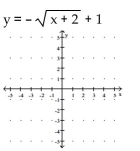
(Multiple Choice)
4.9/5  (37)
(37)
Sketch a graph to represent the situation described.
-Janice jogged twice around a circular race track, which took her 4 minutes, then jogged to the center of the track and rested for 4 minutes before walking home slowly at a constant rate, which took her 12 minutes. Sketch a
Graph of her distance from the center of the race track as a function of time. Assume that the route she takes
Home is a straight line from the center of the race track. 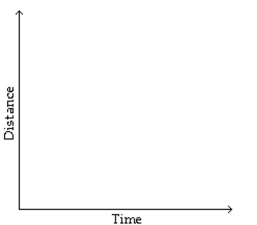
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-Ken is 6 feet tall and is walking away from a streetlight. The streetlight has its light bulb 14 feet above the ground, and Ken is walking at the rate of 5.2 feet per second. Find a function, d(t), which gives the distance Ken
Is from the streetlight in terms of time. Find a function, S(d), which gives the length of Ken's shadow in terms of
D. Then find 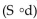 (t). What is the meaning of
(t). What is the meaning of 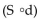 (t)?
(t)?
(Multiple Choice)
4.8/5  (28)
(28)
Determine whether or not the function is one-to-one.
-f(x) = 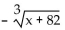
(Multiple Choice)
4.9/5  (27)
(27)
Graph the equation by plotting ordered pairs of numbers.
--2x = y - 1 
(Multiple Choice)
5.0/5  (28)
(28)
Solve the problem.
-A rectangular enclosure must have an area of at least 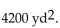 If 260 yd of fencing is to be used, and the width cannot exceed the length, within what limits must the width of the enclosure lie?
If 260 yd of fencing is to be used, and the width cannot exceed the length, within what limits must the width of the enclosure lie?
(Multiple Choice)
4.8/5  (39)
(39)
Evaluate.
-Given f(x) = 4x + 4 and g(x) = 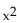 + 6x - 7, find (f ·
+ 6x - 7, find (f ·
(Multiple Choice)
4.8/5  (34)
(34)
Evaluate.
-If f = (2, -6), (5, -3), (6, -1) and g(x) = 4x + 9, find f(5) + g(5).
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-The profit made when t units are sold, t > 0, is given by 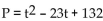 Determine the number of units to be sold for which P < 0 (a loss is taken).
Determine the number of units to be sold for which P < 0 (a loss is taken).
(Multiple Choice)
4.8/5  (29)
(29)
Showing 41 - 60 of 365
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)