Exam 2: Functions and Graphs
Exam 1: Equations, Inequalities, and Modeling531 Questions
Exam 2: Functions and Graphs365 Questions
Exam 3: Polynomial and Rational Functions396 Questions
Exam 4: Exponential and Logarithmic Functions203 Questions
Exam 5: The Trigonometric Functions398 Questions
Exam 6: Trigonometric Identities and Conditional Equations674 Questions
Exam 7: Applications of Trigonometry332 Questions
Exam 8: Systems of Equations and Inequalities293 Questions
Exam 9: Matrices and Determinants218 Questions
Exam 10: The Conic Sections218 Questions
Exam 11: Sequences, Series, and Probability338 Questions
Exam 12: Basic Algebra Review226 Questions
Select questions type
Find the specified domain.
-For f(x) = 2x - 5 and g(x) = 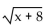 , what is the domain of f + g?
, what is the domain of f + g?
(Multiple Choice)
4.8/5  (31)
(31)
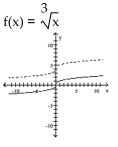
The graph of the given function is drawn with a solid line. The graph of a function, g(x), transformed from this one is
drawn with a dashed line. Find a formula for g(x).
-
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-Assume it costs 25 cents to mail a letter weighing one ounce or less, and then 20 cents for each additional ounce or fraction of an ounce. Let L(x) be the cost of mailing a letter weighing x ounces. Graph y = L(x).
(Multiple Choice)
4.9/5  (40)
(40)
Solve the problem.
-Let C(x) = 600 + 20x be the cost to manufacture x items. Find the average cost per item, to the nearest dollar, to produce 50 items.
(Multiple Choice)
5.0/5  (34)
(34)
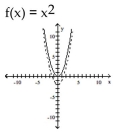
The graph of the given function is drawn with a solid line. The graph of a function, g(x), transformed from this one is
drawn with a dashed line. Find a formula for g(x).
-
(Multiple Choice)
4.9/5  (32)
(32)
Provide an appropriate response.
-Which of the following is a horizontal translation and a reflection of the function 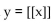 about the x-axis? Use your graphics calculator to verify your result.
about the x-axis? Use your graphics calculator to verify your result.
(Multiple Choice)
4.9/5  (20)
(20)
Solve the problem.
-Elissa wants to set up a rectangular dog run in her backyard. She has 30 feet of fencing to work with and wants to use it all. If the dog run is to be x feet long, express the area of the dog run as a function of x.
(Multiple Choice)
4.9/5  (27)
(27)
Find the requested composition of functions.
-Given f(x) = 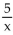 and g(x) =
and g(x) =  find (g
find (g 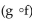 (x).
(x).
(Multiple Choice)
4.7/5  (39)
(39)
Find the requested function value.
-Find 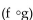 (3) when f(x) = -8x + 1 and g(x) =
(3) when f(x) = -8x + 1 and g(x) = 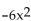 + 8x - 7.
+ 8x - 7.
(Multiple Choice)
4.8/5  (36)
(36)
Find a formula for the inverse of the function described below.
-32° Fahrenheit = 0° Celsius. A function that converts temperatures in Celsius to those in Fahrenheit is f(x) = 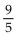 x + 32.
x + 32.
(Multiple Choice)
4.8/5  (30)
(30)
Find the constant of variation and construct the function that is expressed in each statement.
-y varies directly as the square root of x and inversely as w: y = -30.16, when x = 33.64 and w = -0.5.
(Multiple Choice)
4.8/5  (29)
(29)
Solve the problem.
-Suppose a car rental company charges $134 for the first day and $84 for each additional or partial day. Let S(x) represent the cost of renting a car for x days. Find the value of S(4.5).
(Multiple Choice)
4.9/5  (40)
(40)
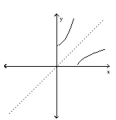
Decide whether or not the functions are inverses of each other.
-
(Multiple Choice)
4.7/5  (32)
(32)
Determine whether the equation defines y as a function of x.
-y = 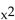 + 3
+ 3
(Multiple Choice)
4.7/5  (38)
(38)
Showing 141 - 160 of 365
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)