Exam 2: Functions and Graphs
Exam 1: Equations, Inequalities, and Modeling531 Questions
Exam 2: Functions and Graphs365 Questions
Exam 3: Polynomial and Rational Functions396 Questions
Exam 4: Exponential and Logarithmic Functions203 Questions
Exam 5: The Trigonometric Functions398 Questions
Exam 6: Trigonometric Identities and Conditional Equations674 Questions
Exam 7: Applications of Trigonometry332 Questions
Exam 8: Systems of Equations and Inequalities293 Questions
Exam 9: Matrices and Determinants218 Questions
Exam 10: The Conic Sections218 Questions
Exam 11: Sequences, Series, and Probability338 Questions
Exam 12: Basic Algebra Review226 Questions
Select questions type
Solve the problem.
-The gravitational attraction A between two masses varies inversely as the square of the distance between them. The force of attraction is 2.25 lb when the masses are 4 ft apart, what is the attraction when the masses are 6 ft
Apart?
(Multiple Choice)
4.7/5  (36)
(36)
Find the indicated composition of functions.
-Let f = (-2, -7), (9, 7) and g = (-7, 9), (4, -9), (6, -7) . Find 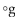
(Multiple Choice)
4.9/5  (33)
(33)
Decide whether or not the functions are inverses of each other.
-f(x) = 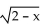 , g(x) = 2 -
, g(x) = 2 - 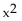
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-The function 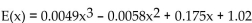 gives the approximate total earnings of a company, in millions of dollars, where x = 0 corresponds to 1996, x = 1 corresponds to 1997, and so on. This model is valid
For the years from 1996 to 2000. Determine the earnings for 1998. Round to the nearest hundredth when
Necessary.
gives the approximate total earnings of a company, in millions of dollars, where x = 0 corresponds to 1996, x = 1 corresponds to 1997, and so on. This model is valid
For the years from 1996 to 2000. Determine the earnings for 1998. Round to the nearest hundredth when
Necessary.
(Multiple Choice)
4.8/5  (36)
(36)
Graph the following function by transforming the given graph of y = f(x).
-Sketch the graph of y = -f(x). 
(Multiple Choice)
4.7/5  (35)
(35)
Find the requested function value.
-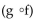 (x): f(x) =
(x): f(x) = 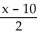 , g(x) = 2x + 10
, g(x) = 2x + 10
(Multiple Choice)
4.8/5  (33)
(33)
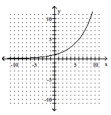
Use the vertical line test to determine whether y is a function of x.
-
(Multiple Choice)
4.9/5  (30)
(30)
Write the equation of the graph after the indicated transformation(s).
-The graph of y = 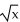 is shifted 2 units to the left. Then the graph is shifted 9 units upward.
is shifted 2 units to the left. Then the graph is shifted 9 units upward.
(Multiple Choice)
4.8/5  (28)
(28)
Determine whether the function is even, odd, or neither.
-f(x) = 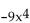 + 5x - 8
+ 5x - 8
(Multiple Choice)
4.8/5  (38)
(38)
Write a formula to express the relationship. Use k as the constant of variation.
-The area of an equilateral triangle varies directly as the square of the side s.
(Multiple Choice)
4.9/5  (33)
(33)
Find the constant of variation and construct the function that is expressed in each statement.
-y varies directly as x: y = 28, when x = 7
(Multiple Choice)
4.8/5  (36)
(36)
Find the requested composition of functions.
-Given f(x) = 6x + 11 and g(x) = 5x - 1, find 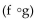 x).
x).
(Multiple Choice)
4.9/5  (26)
(26)
Find the specified domain.
-For f(x) = 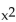 - 16 and g(x) = 2x + 3, what is the domain of g/f?
- 16 and g(x) = 2x + 3, what is the domain of g/f?
(Multiple Choice)
4.9/5  (37)
(37)
Determine whether or not the function is one-to-one.
-f(x) = 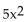 + x
+ x
(Multiple Choice)
4.7/5  (35)
(35)
Determine whether the relation is a function.
-{(-1, -5), (2, 1), (5, -6), (7, 3), (10, 4)}
(Multiple Choice)
4.8/5  (37)
(37)
Determine whether the equation defines y as a function of x.
-y = 2
(Multiple Choice)
4.8/5  (34)
(34)
Showing 121 - 140 of 365
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)