Exam 6: Random Variables and Discrete Probability Distributions
Exam 1: What Is Statistics41 Questions
Exam 2: Graphical and Tabular Descriptive Techniques199 Questions
Exam 3: Numerical Descriptive Techniques226 Questions
Exam 4: Data Collection and Sampling82 Questions
Exam 5: Probability212 Questions
Exam 6: Random Variables and Discrete Probability Distributions174 Questions
Exam 7: Continuous Probability Distributions167 Questions
Exam 8: Sampling Distributions133 Questions
Exam 9: Introduction to Estimation88 Questions
Exam 10: Introduction to Hypothesis Testing186 Questions
Exam 11: Inference About a Population76 Questions
Exam 12: Inference About Comparing Two Populat85 Questions
Exam 13: Inference About Comparing Two Populat85 Questions
Exam 14: Analysis of Variance127 Questions
Exam 15: Chi-Squared Tests118 Questions
Exam 16: Simple Linear Regression and Correlat238 Questions
Exam 17: Multiple Regression147 Questions
Exam 18: Review of Statistical Inference189 Questions
Select questions type
A random variable is a function or rule that assigns a number to each outcome of an experiment.
(True/False)
4.8/5  (34)
(34)
A Poisson random variable is the number of successes that occur in a period of ____________________ or an interval of ____________________ in a Poisson experiment.
(Short Answer)
4.8/5  (26)
(26)
Which of the following is not a required condition for the distribution of a discrete random variable X that can assume values xi ?
(Multiple Choice)
4.8/5  (36)
(36)
Unsafe Levels of Radioactivity The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year. {Unsafe Levels of Radioactivity Narrative} Find the probability that there will be no more than 1 incident in a year.
(Essay)
4.8/5  (37)
(37)
For a random variable X , V ( X + 3)= V ( X + 6), where V refers to the variance.
(True/False)
5.0/5  (29)
(29)
Stress Consider a binomial random variable X with n = 5 and p = 0 . 40, where X represents the number of times in the final exam week a student with 18 credit hours may feel stressed. {Stress Narrative} Find the probability distribution of X .
(Essay)
4.9/5  (34)
(34)
Post Office The number of arrivals at a local post office between 3:00 and 5:00 P.M. has a Poisson distribution with a mean of 12. {Post Office Narrative} Find the probability that the number of arrivals between 3:00 and 5:00 P.M. is at least 10.
(Essay)
4.9/5  (31)
(31)
In the Poisson distribution, the mean is equal to the ____________________.
(Short Answer)
4.8/5  (38)
(38)
Compute the following Poisson probabilities (to 4 decimal places)using the Poisson formula: 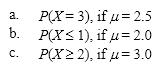
(Essay)
4.9/5  (39)
(39)
Stress Consider a binomial random variable X with n = 5 and p = 0 . 40, where X represents the number of times in the final exam week a student with 18 credit hours may feel stressed. {Stress Narrative} Find P ( X
(Essay)
4.7/5  (37)
(37)
The standard deviation of a binomial random variable X is given by the formula s 2 = np (1 - p ), where n is the number of trials, and p is the probability of success.
(True/False)
4.8/5  (34)
(34)
In a Poisson experiment, the number of successes that occur in any interval of time is ____________________ of the number of success that occur in any other interval.
(Short Answer)
4.8/5  (40)
(40)
The time required to drive from New York to New Mexico is a discrete random variable.
(True/False)
4.9/5  (37)
(37)
Number of Motorcycles The probability distribution of a discrete random variable X is shown below, where X represents the number of motorcycles owned by a family.  {Number of Motorcycles Narrative} Apply the laws of expected value to find the following:
a. E ( X 2)
b. E (2 X 2 + 5)
c. E ( X - 2)2
{Number of Motorcycles Narrative} Apply the laws of expected value to find the following:
a. E ( X 2)
b. E (2 X 2 + 5)
c. E ( X - 2)2
(Essay)
4.7/5  (43)
(43)
In a Poisson distribution, the variance and standard deviation are equal.
(True/False)
4.8/5  (25)
(25)
A community college has 150 word processors. The probability that any one of them will require repair on a given day is 0.025. To find the probability that exactly 25 of the word processors will require repair, one will use what type of probability distribution?
(Multiple Choice)
4.9/5  (41)
(41)
The possible values of a Poisson random variable start at ____________________.
(Short Answer)
4.9/5  (36)
(36)
The dean of students conducted a survey on campus. Grade point average (GPA)is an example of a(n)____________________ random variable.
(Short Answer)
4.9/5  (36)
(36)
Gym Visits Let X represent the number of times a student visits a gym in a one month period. Assume that the probability distribution of X is as follows:  {Gym Visits Narrative} What is the probability that the student visits the gym at most twice in a month?
{Gym Visits Narrative} What is the probability that the student visits the gym at most twice in a month?
(Essay)
4.7/5  (36)
(36)
Showing 41 - 60 of 174
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)