Exam 6: Random Variables and Discrete Probability Distributions
Exam 1: What Is Statistics41 Questions
Exam 2: Graphical and Tabular Descriptive Techniques199 Questions
Exam 3: Numerical Descriptive Techniques226 Questions
Exam 4: Data Collection and Sampling82 Questions
Exam 5: Probability212 Questions
Exam 6: Random Variables and Discrete Probability Distributions174 Questions
Exam 7: Continuous Probability Distributions167 Questions
Exam 8: Sampling Distributions133 Questions
Exam 9: Introduction to Estimation88 Questions
Exam 10: Introduction to Hypothesis Testing186 Questions
Exam 11: Inference About a Population76 Questions
Exam 12: Inference About Comparing Two Populat85 Questions
Exam 13: Inference About Comparing Two Populat85 Questions
Exam 14: Analysis of Variance127 Questions
Exam 15: Chi-Squared Tests118 Questions
Exam 16: Simple Linear Regression and Correlat238 Questions
Exam 17: Multiple Regression147 Questions
Exam 18: Review of Statistical Inference189 Questions
Select questions type
For each of the following random variables, indicate whether the variable is discrete or continuous, and specify the possible values that it can assume.
a. X = the number of traffic accidents in Albuquerque on a given day.
b. X = the amount of weight lost in a month by a randomly selected dieter.
c. X = the average number of children per family in a random sample of 175 families.
d. X = the number of households out of 10 surveyed that own a convection oven.
e. X = the time in minutes required to obtain service in a restaurant.
(Essay)
4.8/5  (40)
(40)
The expected value, E ( X ), of a binomial probability distribution with n trials and probability p of success is:
(Multiple Choice)
4.8/5  (25)
(25)
The number of female customers out of a random sample of 100 customers arriving at a department store has a binomial distribution.
(True/False)
4.8/5  (33)
(33)
The number of homeless people in Boston is an example of a discrete random variable.
(True/False)
4.7/5  (24)
(24)
Shopping Outlet A shopping outlet estimates the probability distribution of the number of stores shoppers actually enter as shown in the table below.  {Shopping Outlet Narrative} Find the variance and standard deviation of the number of stores entered.
{Shopping Outlet Narrative} Find the variance and standard deviation of the number of stores entered.
(Essay)
4.8/5  (39)
(39)
The binomial distribution deals with consecutive trials, each of which has two possible outcomes.
(True/False)
4.9/5  (31)
(31)
A(n)____________________ random variable is one whose values are countable.
(Short Answer)
4.8/5  (36)
(36)
Unsafe Levels of Radioactivity The number of incidents at a nuclear power plant has a Poisson distribution with a mean of 6 incidents per year. {Unsafe Levels of Radioactivity Narrative} Find the probability that there will be at least 1 incident in a year.
(Essay)
4.8/5  (39)
(39)
A motorcycle insurance company evaluates many numerical variables about a person before deciding on an appropriate rate for motorcycle insurance. How long a person has been a licensed rider is an example of a(n)____________________ random variable.
(Short Answer)
4.7/5  (30)
(30)
Retries The following table contains the probability distribution for X = the number of retries necessary to successfully transmit a 1024K data package through a double satellite media.  {Retries Narrative} What is the mean or expected value for the number of retries?
{Retries Narrative} What is the mean or expected value for the number of retries?
(Essay)
4.8/5  (38)
(38)
The number of home insurance policy holders is an example of a discrete random variable
(True/False)
4.9/5  (36)
(36)
In each trial of a binomial experiment, there are ____________________ possible outcomes.
(Short Answer)
4.9/5  (35)
(35)
The expected number of heads in 100 tosses of an unbiased coin is
(Multiple Choice)
4.7/5  (36)
(36)
The amount of milk consumed by a baby in a day is an example of a discrete random variable.
(True/False)
4.8/5  (33)
(33)
The number of customers making a purchase out of 30 randomly selected customers has a Poisson distribution.
(True/False)
4.9/5  (38)
(38)
In Poisson experiment, the probability of more than one success in an interval approaches ____________________ as the interval becomes smaller.
(Short Answer)
5.0/5  (27)
(27)
The weighted average of the possible values that a random variable X can assume, where the weights are the probabilities of occurrence of those values, is referred to as the:
(Multiple Choice)
4.9/5  (28)
(28)
Let X be a Poisson random variable with m = 8. Use the table of Poisson probabilities to calculate: 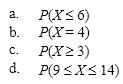
(Essay)
4.9/5  (34)
(34)
Showing 101 - 120 of 174
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)