Exam 28: Determining More Complicated Probabilities
Exam 1: Reasoning About Quantities34 Questions
Exam 2: Numeration Systems96 Questions
Exam 3: Understanding Whole Number Operations66 Questions
Exam 4: Some Conventional Ways of Computing17 Questions
Exam 5: Using Numbers in Sensible Ways38 Questions
Exam 6: Meanings for Fractions85 Questions
Exam 7: Computing With Fractions54 Questions
Exam 8: Multiplicative Comparisons and Multiplicative Reasoning19 Questions
Exam 9: Ratios, Rates, Proportions, and Percents33 Questions
Exam 10: Integers and Other Number Systems24 Questions
Exam 11: Number Theory57 Questions
Exam 12: What Is Algebra28 Questions
Exam 13: A Quantitative Approach to Algebra and Graphing18 Questions
Exam 14: Understanding Change: Relationships Among Time, Distance, and Rate10 Questions
Exam 15: Further Topics in Algebra and Change55 Questions
Exam 16: Polygons75 Questions
Exam 17: Polyhedra51 Questions
Exam 18: Symmetry17 Questions
Exam 19: Tessellations9 Questions
Exam 20: Similarity47 Questions
Exam 21: Curves, Constructions, and Curved Surfaces17 Questions
Exam 22: Transformation Geometry24 Questions
Exam 23: Measurement Basics21 Questions
Exam 24: Area, Surface Area, and Volume27 Questions
Exam 25: Counting Units Fast: Measurement Formulas31 Questions
Exam 26: Special Topics in Measurement21 Questions
Exam 27: Quantifying Uncertainty39 Questions
Exam 28: Determining More Complicated Probabilities37 Questions
Exam 29: Introduction to Statistics and Sampling7 Questions
Exam 30: Representing and Interpreting Data With One Variable32 Questions
Exam 31: Dealing With Multiple Data Sets or With Multiple Variables8 Questions
Exam 32: Variability in Samples21 Questions
Exam 33: Special Topics in Probability16 Questions
Select questions type
In a polling of 400 parents, 20% were high income. One hundred and sixty low-income parents supported vouchers, and 50 high-income parents opposed vouchers. (Hint: Make a table before answering the questions.)
A) What is P(oppose vouchers | high income)? (That is, what is the probability that a parent opposes vouchers, given that the parent has high income?)
B) What is P(high income | oppose vouchers)?
C) What is the probability that a parent has high income OR opposes vouchers?
(Essay)
5.0/5  (42)
(42)
Trisha tosses three fair pennies, but you can't see what happened. She tells you, however, "One or more of the pennies came up heads." What is the probability that Trisha tossed three heads? Write enough to make your thinking clear.
(Essay)
4.7/5  (34)
(34)
Complete the following formulas for special cases, using the most concise answers. (Do not include any unnecessary probabilities.)
A) If A and B are disjoint events, then P(A or B) = _____.
B) If A and B are disjoint events, then P(A and B) = _____.
(Short Answer)
4.9/5  (35)
(35)
If you pick a book at random from the Washington School library, P(red cover) = 0.2 and P(fiction) = 0.4.
A) Find P(red cover and fiction). Show your work for credit.
B) What assumption did you make in part A? Justify your assumption for this situation.
(Essay)
4.8/5  (36)
(36)
Here are data for one community for a year. (Hint: Make a table before answering the questions.) Number of Car Crashes Number of Car Crashes Number of Car Crashes None One or more Male driver 198 9 Female driver 190 3
A) Assuming that the data in the table are typical, what is the probability of a driver having one or more car crashes in a year?
B) Is the probability in part A theoretical or experimental? Explain briefly.
C) What is the probability that the driver is male, given that the driver is in a car crash?
D) What is the probability that the driver is in a car crash, given that the driver is male?
E) What is P(is in one or more car crashes OR is a male)?
(Essay)
4.8/5  (44)
(44)
Two similar cities tried out two programs, P and Q, to cut down on the use of tobacco. They tested the programs with a total of 2000 junior high students. Students used tobacco less or same Students used tobacco more Tobacco program P Tobacco program Q 2000
A) 60% of the 2000 students were in program P. Enter that number of students in the appropriate place in the contingency table.
B) 30% of all the students used tobacco more. Enter that number of students in the appropriate place in the table.
C) of the program Q students used tobacco more. Enter that number of children in the appropriate place in the table.
D) Given that a student was in program P, what is the probability that the student used tobacco less or the same?
E) Given that a student was in program Q, what is the probability that the student used tobacco less or the same?
(Essay)
4.8/5  (36)
(36)
In a certain game you toss two dice. If you roll a 6, you can start the game, and if you roll doubles (both dice with the same number of dots on top), you get an extra turn. Jody is hoping that he will roll a 6 and also get doubles on his next turn. Select the best answer for each item below and explain why you chose that response.
A) Rolling a 6 and rolling doubles are: INDEPENDENT NOT INDEPENDENT
B) Rolling a 6 and rolling doubles are: DISJOINT NOT DISJOINT
(Essay)
4.8/5  (39)
(39)
A) What does it mean to say that A and B are independent events?
B) Give an example of independent events.
(Essay)
4.9/5  (36)
(36)
Of 100 students randomly sampled, 40 are female and 60 are male. A fourth of the females say yes when asked if they have ever driven more than 90 miles/hour, the others say no. But two-thirds of the males say they have and only one-third say no. (Hint: Make a table before answering the questions.)
A) What is the probability that a student chosen at random will say yes to the question?
B) What is the probability that the student is female, given that the student says yes?
C) What is the probability that the student says yes and is female?
D) What is the probability that the student says yes or the student is female (or both)?
(Essay)
4.9/5  (37)
(37)
Three-step experiment: First, randomly choose one of the boxes described below. Then draw one marble. Without replacement, draw another marble from the same box. Note the colors of the two marbles (W = white, R = red).
Box 1 has four white marbles and two red marbles.
Box 2 has six white marbles and two red marbles.
A) Make a complete, condensed tree diagram for the experiment, including the outcomes and their probabilities.
B) What is the probability of at least one red marble?
(Essay)
4.9/5  (35)
(35)
For some unusual two-step experiment, only the data below are given. What is P(XZ)? Write enough (numbers, calculations, words as needed) to make your thinking clear. 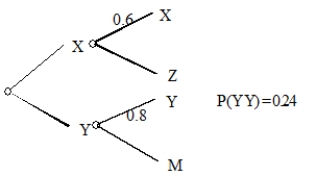
(Essay)
4.8/5  (31)
(31)
For some unusual two-step experiment, only the data below are given. What is P(XZ)? Write enough (numbers, calculations, words as needed) to make your thinking clear. 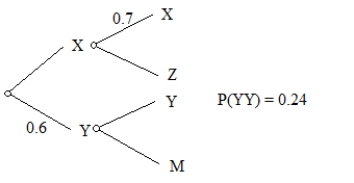
(Essay)
4.9/5  (32)
(32)
If A and B are independent events, P(A or B) = P(A) + P(B) - P(A) ° P(B).
(True/False)
4.9/5  (39)
(39)
In families of six children, the birth order BGGBGB is more probable than the birth order GGGBBB.
(True/False)
4.7/5  (34)
(34)
Showing 21 - 37 of 37
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)