Exam 2: Functions and Graphs
Exam 1: Linear Equations and Graphs59 Questions
Exam 2: Functions and Graphs178 Questions
Exam 3: Mathematics of Finance57 Questions
Exam 4: Systems of Linear Equations; Matrices115 Questions
Exam 5: Linear Inequalities and Linear Programming26 Questions
Exam 6: Linear Programming: The Simplex Method58 Questions
Exam 7: Logic, Sets, and Counting51 Questions
Exam 8: Probability59 Questions
Exam 9: Markov Chains60 Questions
Exam 10: Data Description and Probability Distributions65 Questions
Exam 11: Games and Decisions52 Questions
Exam 12: Appendix A: Basic Algebra Review45 Questions
Exam 13: Appendix B: Special Topics20 Questions
Select questions type
Since life expectancy has increased in the last century, the number of Alzheimer's patients has increased dramatically. The number of patients in the United States reached 4 million in 2000. Using data collected since 2000, it has been found that the data can be modeled by the exponential function 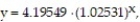 where x is the years since 2000. Estimate the Alzheimer's patients in 2025. Round to the nearest tenth.
where x is the years since 2000. Estimate the Alzheimer's patients in 2025. Round to the nearest tenth.
(Multiple Choice)
4.8/5  (35)
(35)
Determine if the equation specifies a function with independent variable x. If so, find the domain. If not, find a value of x to which there corresponds more than one value of y:
-xy = -5
A) A function with domain all real numbers except x = 0
B) Not a function; for example, when x = -5, y = ±1
(Short Answer)
4.7/5  (40)
(40)
Find the vertex and the maximum or minimum of the quadratic function 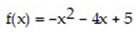 by first writing f in standard form. State the range of f and find the intercepts of f .
by first writing f in standard form. State the range of f and find the intercepts of f .
(Short Answer)
4.9/5  (35)
(35)
Determine if the equation specifies a function with independent variable x. If so, find the domain. If not, find a value of x to which there corresponds more than one value of y:
-x2 + y2 = 36
A) A function with domain ℛ
B) Not a function; for example, when x = 0, y = ±6
(Short Answer)
4.9/5  (38)
(38)
If $4,000 is invested at 7% compounded annually, how long will it take for it to grow to $6,000, assuming no withdrawals are made? Compute answer to the next higher year if not exact.
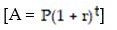
(Multiple Choice)
4.8/5  (36)
(36)
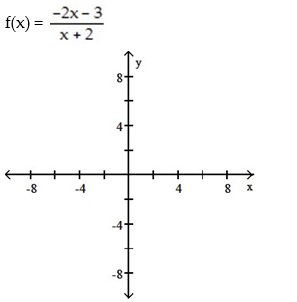
For the rational function below (i) Find the intercepts for the graph; (ii) Determine the domain; (iii) Find any vertical or horizontal asymptotes for the graph; (iv) Sketch any asymptotes as dashed lines. Then sketch the graph of y = f(x).
-
(Multiple Choice)
4.8/5  (29)
(29)
In economics, functions that involve revenue, cost and profit are used. Suppose R(x) and C(x) denote the total revenue and the total cost, respectively, of producing a new high-tech widget. The difference 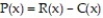 represents the total profit for producing x widgets. Given R(x) = 60x - 0.4
represents the total profit for producing x widgets. Given R(x) = 60x - 0.4 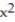 and
and 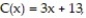 find the equation for P(x).
find the equation for P(x).
(Multiple Choice)
4.7/5  (31)
(31)
Determine whether there is a maximum or minimum value for the given function, and find that value:
-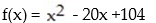
(Multiple Choice)
4.9/5  (40)
(40)
Use a calculator to evaluate the expression. Round the result to five decimal places:
-ln 1097
(Multiple Choice)
4.8/5  (40)
(40)
A professional basketball player has a vertical leap of 37 inches. A formula relating an athlete's vertical leap V, in inches, to hang time T, in seconds, is V= 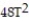 . What is his hang time? Round to the nearest tenth.
. What is his hang time? Round to the nearest tenth.
(Multiple Choice)
4.9/5  (31)
(31)
Use a calculator to evaluate the expression. Round the result to five decimal places:
-ln 0.027
(Multiple Choice)
4.8/5  (37)
(37)
The number of reports of a certain virus has increased exponentially since 1960. The current number of cases can be approximated using the function 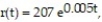 where t is the number of years since 1960. Estimate the of cases in the year 2010.
where t is the number of years since 1960. Estimate the of cases in the year 2010.
(Multiple Choice)
4.8/5  (35)
(35)
Find the vertex form for the quadratic function. Then find each of the following:
(A) Intercepts
(B) Vertex
(C) Maximum or minimum
(D) Range
-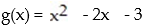
(Multiple Choice)
4.8/5  (42)
(42)
Showing 41 - 60 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)