Exam 16: Multiple Integration
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Use spherical coordinates to find the volume of the indicated region.
-the region inside the solid sphere 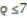 that lies between the cones
that lies between the cones 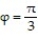 and
and 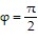
(Multiple Choice)
4.9/5  (38)
(38)
Evaluate the double integral over the given region.
-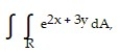 R = {(x, y): 0 x 1, 0 y 1}
R = {(x, y): 0 x 1, 0 y 1}
(Multiple Choice)
4.8/5  (37)
(37)
Use spherical coordinates to find the volume of the indicated region.
-the region enclosed by the cone 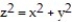 between the planes
between the planes 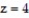 and
and 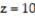
(Multiple Choice)
4.9/5  (36)
(36)
Write an equivalent double integral with the order of integration reversed.
-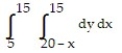
(Multiple Choice)
4.8/5  (35)
(35)
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-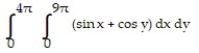
(Multiple Choice)
4.8/5  (36)
(36)
Find the Jacobian for the given transformation
-x = 4u cosh 8v, y = 4u sinh 8v
(Multiple Choice)
4.7/5  (34)
(34)
Provide an appropriate response.
-What does the graph of the equation 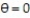 look like?
look like?
(Multiple Choice)
4.8/5  (34)
(34)
Use the given transformation to evaluate the integral.
-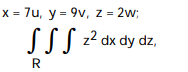 where R is the interior of the ellipsoid
where R is the interior of the ellipsoid 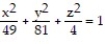
(Multiple Choice)
4.8/5  (41)
(41)
Express the area of the region bounded by the given line(s) and/or curve(s) as an iterated double integral.
-The parabola 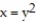 and the line
and the line 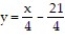
(Multiple Choice)
4.8/5  (30)
(30)
Solve the problem.
-Write an iterated triple integral in the order 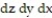 for the volume of the tetrahedron cut from the first octant by the plane
for the volume of the tetrahedron cut from the first octant by the plane 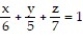 .
.
(Multiple Choice)
4.7/5  (31)
(31)
Evaluate the integral by changing the order of integration in an appropriate way.
-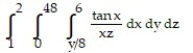
(Multiple Choice)
5.0/5  (41)
(41)
Reverse the order of integration and then evaluate the integral.
-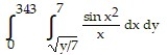
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-Find the average distance from a point 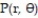 in the region bounded by
in the region bounded by 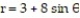 to the origin.
to the origin.
(Multiple Choice)
4.8/5  (38)
(38)
Reverse the order of integration and then evaluate the integral.
-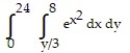
(Multiple Choice)
5.0/5  (37)
(37)
Showing 121 - 140 of 299
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)