Exam 16: Multiple Integration
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Find the area of the region specified in polar coordinates.
-the region enclosed by the curve r = 4 sin 2
(Multiple Choice)
4.7/5  (35)
(35)
Choose the one alternative that best completes the statement or answers the question. Evaluate the integral
-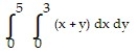
(Multiple Choice)
4.9/5  (31)
(31)
Find the volume of the indicated region.
-the region that lies under the paraboloid 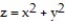 and above the triangle enclosed by the lines
and above the triangle enclosed by the lines 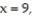
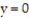 , and
, and 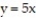
(Multiple Choice)
4.8/5  (38)
(38)
Find the volume under the surface z = f(x,y) and above the rectangle with the given boundaries.
-z = 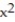 +
+ 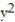 ; R = {(x, y): 0 x 1, 0 y 1}
; R = {(x, y): 0 x 1, 0 y 1}
(Multiple Choice)
4.8/5  (30)
(30)
Find the center of mass of a thin plate of constant density covering the given region.
-The region bounded by the x-axis and the semicircle y = 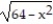
(Multiple Choice)
5.0/5  (38)
(38)
Solve the problem.
-Let D be the region that is bounded below by the cone 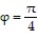 and above by the sphere
and above by the sphere 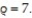 Set up the triple integral for the volume of D in cylindrical coordinates.
Set up the triple integral for the volume of D in cylindrical coordinates.
(Multiple Choice)
4.9/5  (37)
(37)
Evaluate the double integral over the given region.
-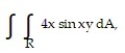 R = {(x, y): 0 x , 0 y 1}
R = {(x, y): 0 x , 0 y 1}
(Multiple Choice)
4.8/5  (31)
(31)
Find the volume of the indicated region.
-the region bounded by the paraboloid 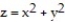 , the cylinder
, the cylinder 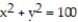 , and the
, and the 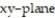
(Multiple Choice)
4.7/5  (25)
(25)
Solve the problem.
-Find the average distance from a point 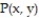 in the first two quadrants of the disk
in the first two quadrants of the disk 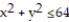 to the origin.
to the origin.
(Multiple Choice)
4.9/5  (44)
(44)
Find the area of the region specified in polar coordinates.
-the region enclosed by the curve r = 9 cos 3
(Multiple Choice)
4.9/5  (38)
(38)
Find the center of mass of a thin plate of constant density covering the given region.
-The region bounded by the parabola y = 9 - 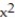 and the x-axis
and the x-axis
(Multiple Choice)
4.8/5  (29)
(29)
Use the given transformation to evaluate the integral.
-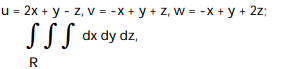 where R is the parallelepiped bounded by the planes
where R is the parallelepiped bounded by the planes 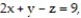
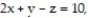
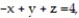
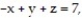
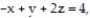
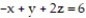
(Multiple Choice)
4.9/5  (33)
(33)
Find the center of mass of a thin plate of constant density covering the given region.
-The region bounded by y = 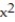 and y = 3
and y = 3
(Multiple Choice)
4.7/5  (41)
(41)
Evaluate the integral by changing the order of integration in an appropriate way.
-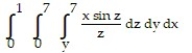
(Multiple Choice)
4.8/5  (36)
(36)
Change the order of integration and evaluate the integral.
-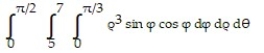
(Multiple Choice)
4.9/5  (42)
(42)
Evaluate the integral by changing the order of integration in an appropriate way.
-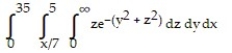
(Multiple Choice)
4.9/5  (31)
(31)
Find the average value of the function f over the given region.
-f(x, y) = 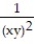 ; R = {(x, y): 1 x 5, 1 y 5}
; R = {(x, y): 1 x 5, 1 y 5}
(Multiple Choice)
4.7/5  (37)
(37)
Showing 61 - 80 of 299
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)