Exam 16: Multiple Integration
Exam 1: Functions226 Questions
Exam 2: Limits224 Questions
Exam 3: Derivatives367 Questions
Exam 4: Applications of the Derivative228 Questions
Exam 5: Integration166 Questions
Exam 6: Applications of Integration211 Questions
Exam 7: Logarithmic, Exponential, and Hyperbolic Functions85 Questions
Exam 8: Integration Techniques287 Questions
Exam 9: Differential Equations76 Questions
Exam 10: Sequences and Infinite Series173 Questions
Exam 11: Power Series103 Questions
Exam 12: Parametric and Polar Curves169 Questions
Exam 13: Vectors and the Geometry of Space131 Questions
Exam 14: Vector-Valued Functions83 Questions
Exam 15: Functions of Several Variables229 Questions
Exam 16: Multiple Integration299 Questions
Exam 17: Vector Calculus173 Questions
Select questions type
Find the average value of the function f over the given region.
-f(x, y) = 2x + 8y; R = {(x, y): 0 x 1, 0 y 1}
(Multiple Choice)
4.9/5  (42)
(42)
Find the average value of the function f over the given region.
-f(x, y) = 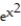 over the region bounded by
over the region bounded by 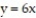 ,
, 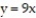 ,
, 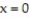 , and
, and 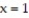 .
.
(Multiple Choice)
4.8/5  (40)
(40)
Find the volume of the indicated region.
-the region bounded by the paraboloid 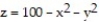 and the xy-plane
and the xy-plane
(Multiple Choice)
4.9/5  (36)
(36)
Change the Cartesian integral to an equivalent polar integral, and then evaluate.
-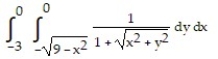
(Multiple Choice)
5.0/5  (30)
(30)
Solve the problem.
-Set up the triple integral for the volume of the sphere 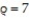 in spherical coordinates.
in spherical coordinates.
(Multiple Choice)
4.7/5  (35)
(35)
Provide an appropriate response.
-What does the graph of the equation 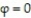 look like?
look like?
(Multiple Choice)
4.8/5  (32)
(32)
Change the Cartesian integral to an equivalent polar integral, and then evaluate.
-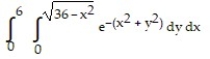
(Multiple Choice)
4.9/5  (42)
(42)
Find the area of the region specified in polar coordinates.
-one petal of the rose curve r = 9 sin 2
(Multiple Choice)
4.9/5  (38)
(38)
Change the order of integration and evaluate the integral.
-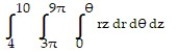
(Multiple Choice)
4.7/5  (40)
(40)
Provide an appropriate response.
-What does the graph of the equation  look like?
look like?
(Multiple Choice)
4.8/5  (33)
(33)
Change the order of integration and evaluate the integral.
-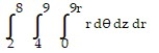
(Multiple Choice)
4.8/5  (40)
(40)
Find the volume of the indicated region.
-the region that lies under the plane 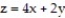 and over the triangle with vertices at
and over the triangle with vertices at 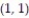 ,
, 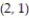 , and
, and 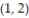
(Multiple Choice)
4.9/5  (38)
(38)
Find the center of mass of a thin plate of constant density covering the given region.
-The region bounded by the x-axis and the curve y = 7sin x, 0 x
(Multiple Choice)
4.7/5  (31)
(31)
Find the center of mass of a thin plate covering the given region with the given density function.
-The region between the x-axis and the curve y = 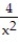 , 1 x 2, with density (x) =
, 1 x 2, with density (x) = 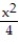
(Multiple Choice)
4.8/5  (39)
(39)
Find the average value of over the given region. 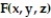 -
-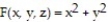 +
+  over the cube in the first octant bounded by the coordinate planes and the planes
over the cube in the first octant bounded by the coordinate planes and the planes 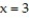
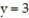
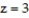 ,,
,,
(Multiple Choice)
4.7/5  (42)
(42)
Use spherical coordinates to find the volume of the indicated region.
-the region enclosed by the sphere 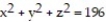 and the cylinder
and the cylinder 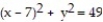
(Multiple Choice)
4.8/5  (34)
(34)
Showing 161 - 180 of 299
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)