Exam 8: Random Variables

Sara is a frequent business traveler. For security purposes, 10% of all people boarding airplanes are randomly selected for additional screening just prior to boarding. Define the random variable X = number of flights Sara completes before being chosen for additional screening. For instance, if she is searched boarding her next flight, then X = 0. What is the value of P(X = 2) = probability Sara completes two flights without screening and then is chosen for additional screening on the next one?

Suppose that X and Y are independent binomial random variables described in the table below. 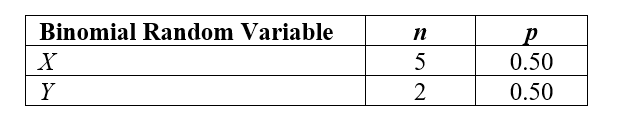Let W = X + Y. Find the probability that W = 4.

Suppose that for X = net amount won or lost in a lottery game, the expected value is E(X) = -$0.50. What is the correct interpretation of this value?

Use the following information for questions: Suppose that a student needs to buy 6 books for her history course. The number of books that she will be able to find used is a binomial random variable X with n = 6 and p = 0.30. In other words, the probability that she will find any given book used is 0.30, and is independent from one book to the next. -What is the expected number of used books she will find, E(X)?

Use the following information for questions: Some managers of companies use employee rankings to laud the best and let go of the worst. Suppose the distribution of rankings of employees at a large company is normal with a mean of 65 points and a standard deviation of 6 points. -What proportion of employees has a ranking above 59 points?

Use the following information for questions: John and Mary both leave for class at the same time. The time it takes them to get to class, (J = time for John, M = time for Mary) are independent normal random variables. For John, the mean time E(J) = 10 minutes with variance V(J) = 4 minutes. For Mary, the mean time E(M) = 8 minutes with variance V(M) = 1 minute. -What is the probability that John will get to class before Mary does?

Use the following information for questions: In a family with 4 children, the number of children with blue eyes is a binomial random variable X with n = 4 and p = .20. -What is the probability that none of the children will have blue eyes?

Use the following information for questions: Joan has noticed that the probability distribution for X = number of students in line to use the campus ATM machine when she shows up to use it is shown below. -What is the probability that there will be no more than 1 student in line when Joan shows up?

Consider an experiment that involves repeatedly rolling a six-sided die. Which of the following is a binomial random variable?

Use the following information for questions: A bank offers free coffee to its customers. The coffee is brewed each morning in a large coffee urn, and the amount brewed varies slightly. It is independent from day to day, with mean of 125 ounces and standard deviation of 3 ounces. The amount customers drink from day to day is also random, with mean of 100 ounces and standard deviation of 5 ounces, and is independent of the amount brewed. -What is the mean and standard deviation for the amount of coffee remaining at the end of the day?

The time taken to deliver a pizza has a uniform probability distribution from 20 minutes to 60 minutes. What is the probability that the time to deliver a pizza is at least 25 minutes?

The normal approximation to the binomial distribution is most useful for finding which of the following?

Use the following information for questions: Did high gas prices keep Americans from hitting the road this past summer? In a nationwide survey of adults, one variable measured was how many days vacationers spent driving on the road on their longest trip. Consider the following (partial) probability distribution for the random variable X = the number of days for the longest car trip. -Suppose the probability of 7 days is twice as likely as the probability of 8 days. What are the two missing probabilities to complete the distribution for X?

Use the following information for questions: The Southside Bowling Alley has collected data on the number of children that come to birthday parties held at the bowling alley. Let the random variable X = the number of children per party. The distribution for the random variable X is given below. -What is the probability that at least 7 children will come to a party?

A medication produces side effects in each user with probability 0.10 and this is independent from one person to the next. If 50 people use the medication, the number who will experience side effects is

Use the following information for questions: For each situation, decide if the random variable described is a discrete random variable or a continuous random variable. -Random variable X = the weight (in pounds) a dieter will lose after following a two week weight loss program.

Use the following information for questions: The probability distribution for X = number of heads in 4 tosses of a fair coin is partially given in the table below. -What is the probability of getting 1 or 2 heads?

Use the following information for questions: The average time taken to complete an exam, X, follows a normal probability distribution with mean = 60 minutes and standard deviation 30 minutes. -What is the probability that a randomly chosen student will complete the exam in 30 minutes or less?

Heights of college women have a distribution that can be approximated by a normal curve with a mean of 65 inches and a standard deviation equal to 3 inches. About what proportion of college women are between 65 and 67 inches tall?

Use the following information for questions: Centerpieces are normally distributed with mean of 30 ounces and standard deviation of2 ounces. The weights of the shipping boxes are normally distributed with mean of 12 ounces and standard deviation of 1 ounce. Suppose that centerpieces are chosen at random and packed into randomly chosen shipping boxes. -If a package exceeds 45 ounces, an additional charge is incurred. What is the proportion of packages will incur such a charge?