Exam 4: Exponential and Logarithmic Functions
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Express the following in terms of and , where and . For example, .
-
(Multiple Choice)
4.9/5  (30)
(30)
Solve the problem.
-The number of books in a small library increases according to the function , where is measured in years. How many books will the library have after 7 years?
(Multiple Choice)
4.9/5  (42)
(42)
Solve the problem.
-A certain radioactive isotope decays at a rate of annually. Determine the half-life of this isotope, to the nearest year.
(Multiple Choice)
4.9/5  (29)
(29)
without graphing, describe the shape of the graph of the function and complete the ordered pairs and ,
-
(Multiple Choice)
4.8/5  (41)
(41)
Solve the problem.
-The number of books in a small library increases according to the function , where is measured in years. How many books will the library have after 3 years?
(Multiple Choice)
4.8/5  (31)
(31)
Write the logarithmic and exponential equations associated with the display.
-
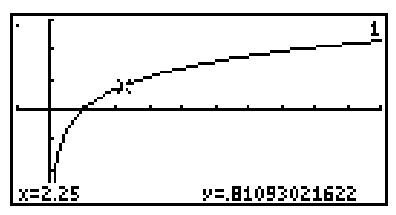
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-A certain noise measures 113 decibels. If the intensity is multiplied by 10 , how many decibels will the new noise measure? Use the formula , where .
(Multiple Choice)
4.9/5  (32)
(32)
Solve the problem.
-The number of years since two independently evolving languages split off from a common ancestral language is approximated by , where is the percent of words from the ancestral language common to both languages now. Find if two languages split about 1530 years ago. Round to the nearest percent.
(Multiple Choice)
4.8/5  (41)
(41)
Solve.
-In recent years, many states have passed laws against smoking in public buildings. The total number of states that have passed a no smoking in public buildings law, years after 1985 is given by the function
How many states had passed the law in 1985 ?
(Multiple Choice)
4.9/5  (30)
(30)
Write the expression as a sum and/or a difference of logarithms with all variables to the first degree.
-
(Multiple Choice)
4.9/5  (28)
(28)
Classify the function as a linear, quadratic, or exponential.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-The height in meters of women of a certain tribe is approximated by where is the woman's age in years and . Estimate the height (to the nearest hundredth of a meter) of a woman of the tribe 4 years of age.
(Multiple Choice)
4.7/5  (36)
(36)
Provide an appropriate response.
-In your own words, explain what a logarithm is.
(Essay)
4.9/5  (42)
(42)
Showing 21 - 40 of 192
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)