Exam 4: Exponential and Logarithmic Functions
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Write the logarithmic and exponential equations associated with the display.
-
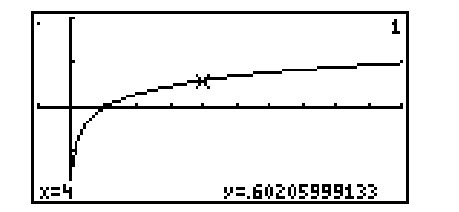
(Multiple Choice)
4.9/5  (39)
(39)
Provide an appropriate response.
-How can you use the change-of-base rule for logarithms to help solve the equation 5 = 3x?
(Essay)
4.7/5  (37)
(37)
Solve the problem.
-An artifact is discovered at a certain site. If it has of the carbon-14 it originally contained, what is the approximate age of the artifact to the nearest year? (carbon-14 decays at the rate of annually.)
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-A certain noise produces of power. What is the decibel level of this noise (to nearest decibel)? Use the formula , where watt .
(Multiple Choice)
4.8/5  (36)
(36)
Write the logarithmic and exponential equations associated with the display.
-
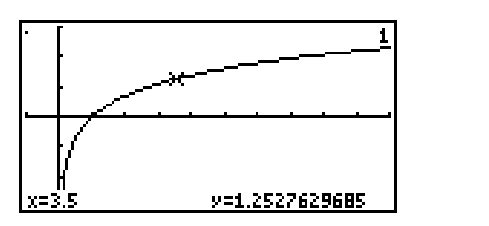
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-The growth in the population of a certain rodent at a dump site fits the exponential function , where is the number of years since 1967. Estimate the population in the year 2000.
(Multiple Choice)
4.9/5  (31)
(31)
Solve the problem.
-How long will it take for the population of a certain country to double if its annual growth rate is 6.1? (Round to the nearest year.)
(Multiple Choice)
4.8/5  (31)
(31)
Write the expression as a sum and/or a difference of logarithms with all variables to the first degree.
-
(Multiple Choice)
4.9/5  (33)
(33)
Showing 81 - 100 of 192
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)