Exam 12: Applications of the Derivative
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Find the largest open intervals where the function is concave upward.
-
(Multiple Choice)
4.7/5  (32)
(32)
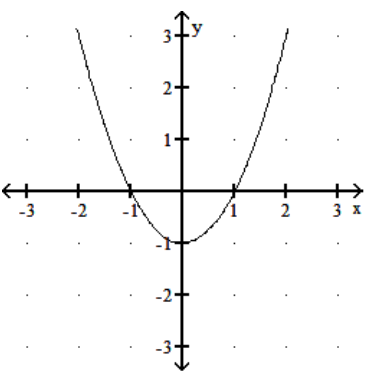
The graph of the derivative function is given. Find the critical numbers of the function .
-
(Multiple Choice)
4.7/5  (42)
(42)
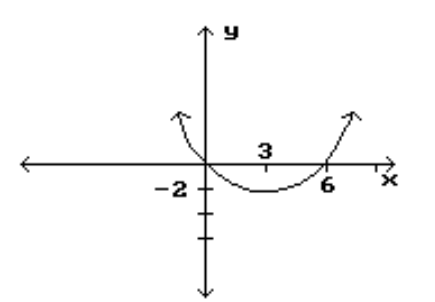
Find the location and value of each local extremum for the function.
-
(Multiple Choice)
4.9/5  (43)
(43)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.7/5  (41)
(41)
Find the absolute extremum within the specified domain.
-Minimum of
(Multiple Choice)
4.8/5  (46)
(46)
Sketch a graph of a single function that has these properties.
-(a) defined for all real numbers
(b) decreasing on
(c) increasing on
(d) concave downward on
(e) is undefined
(Essay)
4.9/5  (37)
(37)
Find the dimensions that produce the maximum floor area for a one-story house that is rectangular in shape and has a perimeter of .
(Multiple Choice)
4.8/5  (36)
(36)
Find the location of the indicated absolute extrema for the function.
-Maximum
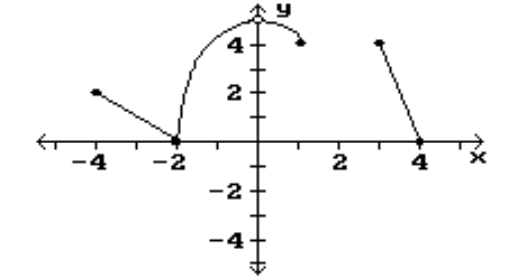
(Multiple Choice)
4.8/5  (45)
(45)
Find the coordinates of the points of inflection for the function.
-
(Multiple Choice)
4.9/5  (44)
(44)
Find the location of the indicated absolute extrema for the function.
-Minimum 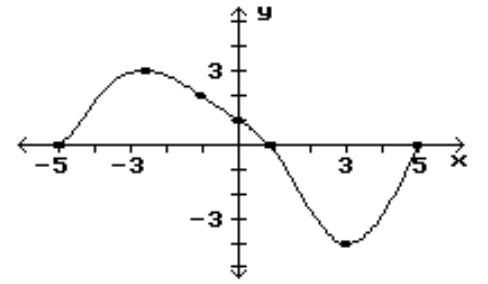
(Multiple Choice)
4.9/5  (33)
(33)
Find the absolute extremum within the specified domain.
-Maximum of ;
(Multiple Choice)
4.9/5  (39)
(39)
If the price charged for a candy bar is cents, then thousand candy bars will be sold in a certain city, where . How many candy bars must be sold to maximize revenue?
(Multiple Choice)
5.0/5  (42)
(42)
Solve the problem.
-Given the revenue and cost functions and , where is the daily production, find the rate of change of profit with respect to time when 15 units are produced and the rate of change of production is 4 units per day.
(Multiple Choice)
5.0/5  (34)
(34)
Solve the problem.
-A truck burns fuel at the rate (gallons per hr) of while traveling at . If fuel costs per gallon, find the speed that minimizes total cost for a 200 -mile trip. Round to the nearest tenth.
(Multiple Choice)
4.8/5  (38)
(38)
Find the largest open intervals where the function is concave upward.
-
(Multiple Choice)
4.9/5  (32)
(32)
Solve each problem.
-An architect needs to design a rectangular room with an area of . What dimensions should she use in order to minimize the perimeter?
(Multiple Choice)
4.8/5  (43)
(43)
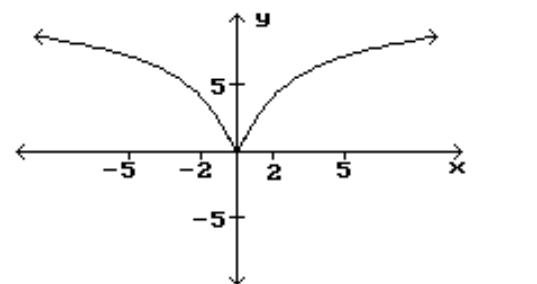
Find the location and value of each local extremum for the function.
-
(Multiple Choice)
4.8/5  (34)
(34)
Solve the problem.
-A company knows that unit cost and unit revenue from the production and sale of units are related by . Find the rate of change of revenue per unit when the cost per unit is changing by and the revenue is .
(Multiple Choice)
5.0/5  (38)
(38)
Find the largest open intervals where the function is concave upward.
- (exact values)
(Multiple Choice)
4.9/5  (36)
(36)
Showing 161 - 180 of 220
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)