Exam 12: Applications of the Derivative
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Solve the problem.
-A company is constructing an open-top, square-based, rectangular metal tank that will have a volume of . What dimensions yield the minimum surface area? Round to the nearest tenth, if necessary.
(Multiple Choice)
4.9/5  (36)
(36)
Solve the problem.
-The position of a particle at time is given by , where . Find the velocity .
(Multiple Choice)
4.9/5  (37)
(37)
If the price charged for a bolt is cents, then thousand bolts will be sold in a certain hardware store, where . How many bolts must be sold to maximize revenue?
(Multiple Choice)
4.8/5  (24)
(24)
Solve the problem.
-It is estimated that the total value of a stamp collection is given by the formula , where is the number of years from now. If the inflation rate is running continuously at per year so that the (discounted) present value of an item that will be worth in years' time is given by . Sketch the graph of the discounted value as a function of time at which the stamp collection is sold. The graph has one local minimum. What is the value of at the local minimum? What is the discounted value of the collection at that time?
(Multiple Choice)
4.9/5  (34)
(34)
Find all critical numbers for the function. State whether it leads to a local maximum, a local minimum, or neither.
-
(Multiple Choice)
4.9/5  (46)
(46)
Identify the intervals where the function is changing as requested.
-Decreasing
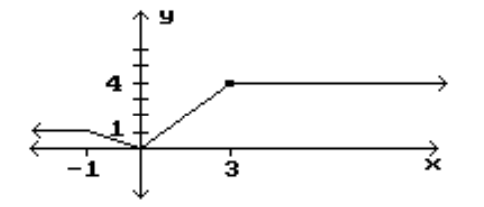
(Multiple Choice)
4.8/5  (38)
(38)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.9/5  (40)
(40)
Find the largest open interval where the function is changing as requested.
-Increasing
(Multiple Choice)
4.8/5  (36)
(36)
Find the location of the indicated absolute extrema for the function.
-Maximum
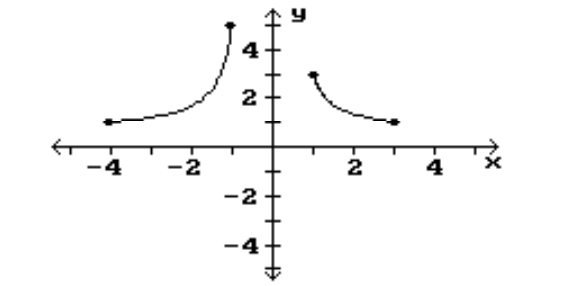
(Multiple Choice)
4.8/5  (37)
(37)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.8/5  (36)
(36)
Find the absolute extremum within the specified domain.
-Maximum of
(Multiple Choice)
4.8/5  (36)
(36)
Find the location of the indicated absolute extrema for the function.
-Maximum
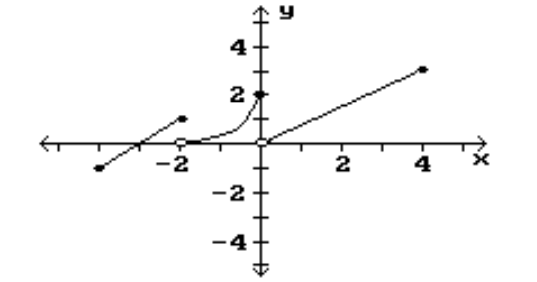
(Multiple Choice)
4.8/5  (35)
(35)
Determine the location of each local extremum of the function.
-
(Multiple Choice)
4.9/5  (44)
(44)
Showing 101 - 120 of 220
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)