Exam 12: Applications of the Derivative
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Identify the intervals where the function is changing as requested.
-Decreasing
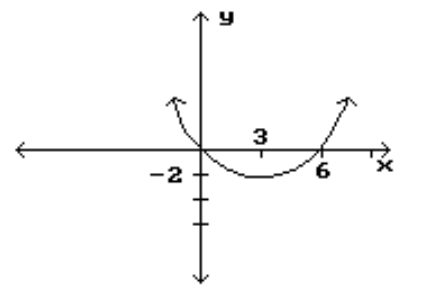
(Multiple Choice)
4.9/5  (40)
(40)
Use calculus and a graphing calculator to find the approximate location of all relative extrema.
-
(Multiple Choice)
4.8/5  (43)
(43)
Solve each problem.
-Find two numbers whose sum is 440 and whose product is as large as possible.
(Multiple Choice)
4.8/5  (35)
(35)
Find the location of the indicated absolute extrema for the function.
-Maximum
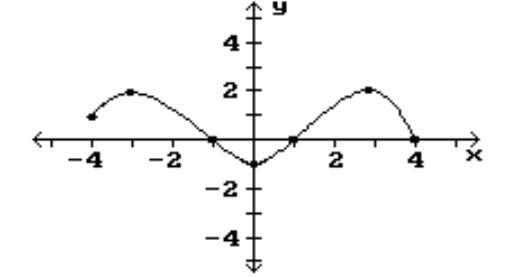
(Multiple Choice)
4.9/5  (37)
(37)
Find the absolute extremum within the specified domain.
-Minimum of
(Multiple Choice)
4.9/5  (36)
(36)
Find all critical numbers for the function. State whether it leads to a local maximum, a local minimum, or neither.
-
(Multiple Choice)
4.9/5  (39)
(39)
Sketch the graph and show all local extrema and inflection points.
-
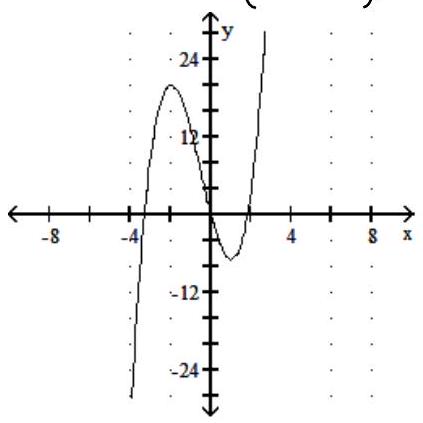
(Multiple Choice)
4.9/5  (43)
(43)
A private shipping company will accept a box for domestic shipment only if the sum of its length and girth (distance around) does not exceed . Suppose you want to mail a box with square sides so that its dimensions are by by and it's girth is . What dimensions will give the box its largest volume?
(Multiple Choice)
4.9/5  (41)
(41)
Identify the intervals where the function is changing as requested.
-Increasing
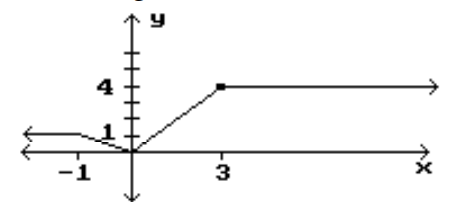
(Multiple Choice)
4.9/5  (38)
(38)
Find the coordinates of the points of inflection for the function.
-
(Multiple Choice)
4.7/5  (25)
(25)
Find the coordinates of the points of inflection for the function.
-
(Multiple Choice)
4.8/5  (38)
(38)
Identify the intervals where the function is changing as requested.
-Increasing
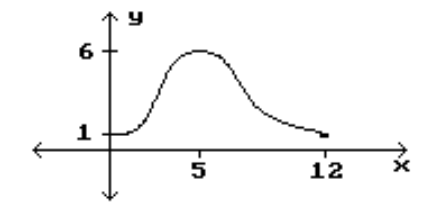
(Multiple Choice)
4.9/5  (42)
(42)
Solve the problem.
-Because of material shortages, it is increasingly expensive to produce 6.0L diesel engines. In fact, the profit in millions of dollars from producing hundred thousand engines is approximated by , where . Find the point of diminishing returns.
(Multiple Choice)
4.8/5  (39)
(39)
Identify the intervals where the function is changing as requested.
-Decreasing
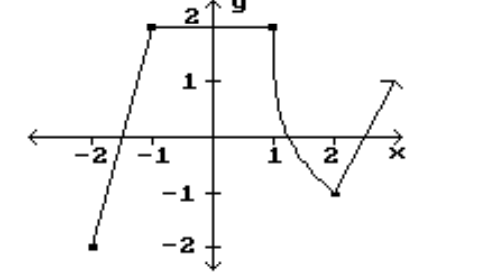
(Multiple Choice)
4.9/5  (46)
(46)
Solve the problem.
-The cost function for the manufacture of graphing calculators is given by , where is the number of graphing calculators manufactured.
Using the appropriate domain, sketch the graph of the average cost to manufacture graphing calculators. Find the absolute minimum on the graph of . What do the coordinates of the absolute minimum tell us?
(Multiple Choice)
4.7/5  (39)
(39)
is the distance (in ) traveled in time (in s) by a particle. Find the velocity and acceleration at the given time.
-
(Multiple Choice)
4.8/5  (33)
(33)
Find the largest open intervals where the function is concave upward.
-
(Multiple Choice)
4.8/5  (45)
(45)
Solve the problem.
-A zoom lens in a camera makes a rectangular image on the film that is . As the lens zooms in and out, the size of the image changes. Find the rate at which the area of the image begins to change if the length of the frame changes at and the width of the frame changes at .
(Multiple Choice)
4.8/5  (30)
(30)
Find the coordinates of the points of inflection for the function.
-
(Multiple Choice)
4.9/5  (32)
(32)
Showing 121 - 140 of 220
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)