Exam 12: Applications of the Derivative
Exam 1: Algebra and Equations409 Questions
Exam 2: Graphs, Lines, and Inequalities255 Questions
Exam 3: Functions and Graphs323 Questions
Exam 4: Exponential and Logarithmic Functions192 Questions
Exam 5: Mathematics of Finance183 Questions
Exam 6: Systems of Linear Equations and Matrices215 Questions
Exam 7: Linear Programming203 Questions
Exam 8: Sets and Probability240 Questions
Exam 9: Counting, Probability Distributions, and Further Topics in Probability210 Questions
Exam 10: Introduction to Statistics169 Questions
Exam 11: Differential Calculus342 Questions
Exam 12: Applications of the Derivative220 Questions
Exam 13: Integral Calculus227 Questions
Exam 14: Multivariate Calculus152 Questions
Select questions type
Solve the problem.
-A company wishes to manufacture a box with a volume of 16 cubic feet that is open on top and is twice as long as it is wide. Find the width to the nearest foot of the box that can be produced using the minimum amount of material.
(Multiple Choice)
4.9/5  (43)
(43)
is the distance (in ) traveled in time (in s) by a particle. Find the velocity and acceleration at the given time.
-
(Multiple Choice)
4.9/5  (38)
(38)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.9/5  (37)
(37)
is the distance (in ) traveled in time (in s) by a particle. Find the velocity and acceleration at the given time.
-
(Multiple Choice)
4.7/5  (33)
(33)
Solve the problem.
-The energy cost of a speed burst as a function of the body weight of a dolphin is given by , where is the weight of the dolphin (in ) and is the energy expenditure (in ). Suppose that the weight of a dolphin is increasing at a rate of . Find the rate at which the energy expenditure is changing with respect to time.
(Multiple Choice)
4.9/5  (33)
(33)
Determine the location of each local extremum of the function.
-
(Multiple Choice)
4.9/5  (36)
(36)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.8/5  (42)
(42)
Solve the problem.
-From a thin piece of cardboard 40 in. by 40 in., square corners are cut out so that the sides can be folded up to make a box. What dimensions will yield a box of maximum volume? What is the maximum volume? Round to the nearest tenth, if necessary.
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-The cost of a computer system increases with increased processor speeds. The cost of a system as a function of processor speed is estimated as , where is the processor speed in MHz. Find the processor speed for which cost is at a minimum. Round to the nearest tenth if necessary.
(Multiple Choice)
4.8/5  (32)
(32)
Use the first derivative test to determine the location of each local extremum and the value of the function at thatextremum.
-
(Multiple Choice)
4.9/5  (41)
(41)
Solve each problem.
-The price of a certain computer system decreases immediately after its introduction and then increases. If the price is estimated by the formula , where is the time in months from its introduction, find the time until the minimum price is reached.
(Multiple Choice)
4.9/5  (48)
(48)
Solve the problem.
-It is estimated that the total value of a stamp collection is given by the formula , where is the number of years from now. If the inflation rate is running continuously at per year so that the (discounted) present value of an item that will be worth in years' time is given by . Sketch the graph of the discounted value as a function of time at which the stamp collection is sold. The graph has an absolute maximum at , and a local maximum at one other point. What is the value of at the local maximum? What is the discounted value of the collection at that time?
(Multiple Choice)
4.8/5  (28)
(28)
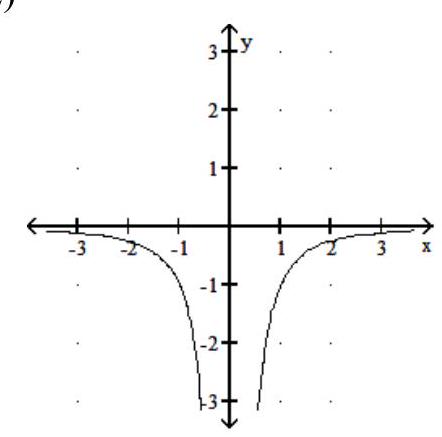
The graph of the derivative function is given. Find the critical numbers of the function .
-
(Multiple Choice)
4.8/5  (37)
(37)
Solve the problem.
-The cost function for the manufacture of graphing calculators is given by , where is the number of graphing calculators manufactured. Using the appropriate domain, sketch the graph of the average cost to manufacture graphing calculators. What is the significance of ?
(Multiple Choice)
4.9/5  (41)
(41)
Find the location of the indicated absolute extrema for the function.
-Minimum
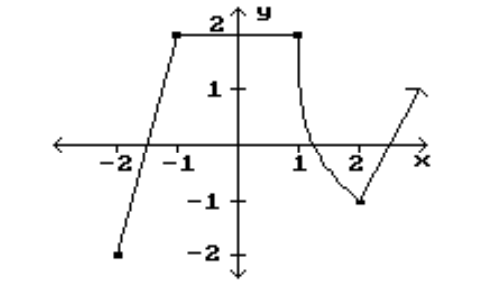
(Multiple Choice)
4.8/5  (37)
(37)
Solve each problem.
-If the price charged for a bolt is cents, then thousand bolts will be sold in a certain hardware store, where . How many bolts must be sold to maximize revenue?
(Multiple Choice)
4.8/5  (42)
(42)
Use the first derivative test to determine the location of each local extremum and the value of the function at thatextremum.
-
(Multiple Choice)
4.9/5  (34)
(34)
Sketch the graph and show all local extrema and inflection points.
-
(Multiple Choice)
5.0/5  (37)
(37)
Find the coordinates of the points of inflection for the function.
-
(Multiple Choice)
4.8/5  (29)
(29)
Showing 81 - 100 of 220
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)