Exam 22: Linear Programming
Exam 1: Operations and Productivity126 Questions
Exam 2: Operations Strategy in a Global Environment135 Questions
Exam 3: Project Management123 Questions
Exam 4: Forecasting144 Questions
Exam 5: Design of Goods and Services137 Questions
Exam 6: Managing Quality130 Questions
Exam 7: Statistical Process Control154 Questions
Exam 8: Process Strategy131 Questions
Exam9: Capacity and Constraint Management107 Questions
Exam 10: Location Strategies140 Questions
Exam 11: Layout Strategies161 Questions
Exam 12: Human Resources, Job Design, and Work Measurement191 Questions
Exam 13: Supply-Chain Management145 Questions
Exam 14: Outsourcing as a Supply-Chain Strategy73 Questions
Exam 15: Inventory Management155 Questions
Exam 16: Aggregate Planning134 Questions
Exam 17: Material Requirements Planning MRP and ERP169 Questions
Exam 18: Short-Term Scheduling139 Questions
Exam 19: Just-In-Time and Lean Options137 Questions
Exam 20: Maintenance and Reliability130 Questions
Exam 21: Decision-Making Tools97 Questions
Exam 22: Linear Programming100 Questions
Exam 23: Transportation Models94 Questions
Exam 24: Waiting-Line Models135 Questions
Exam 25: Learning Curves111 Questions
Exam 26: Simulation93 Questions
Select questions type
One requirement of a linear programming problem is that the objective function must be expressed as a linear equation.
(True/False)
4.9/5  (40)
(40)
The Queen City Nursery manufactures bags of potting soil from compost and topsoil. Each cubic foot of compost costs 12 cents and contains 4 pounds of sand, 3 pounds of clay, and 5 pounds of humus. Each cubic foot of topsoil costs 20 cents and contains 3 pounds of sand, 6 pounds of clay, and 12 pounds of humus. Each bag of potting soil must contain at least 12 pounds of sand, 12 pounds of clay, and 10 pounds of humus. Explain how this problem meets the conditions of a linear programming problem. Plot the constraints and identify the feasible region. Graphically or with corner points find the best combination of compost and topsoil that meets the stated conditions at the lowest cost per bag. Identify the lowest cost possible.
(Essay)
4.8/5  (31)
(31)
Lost Maples Winery makes three varieties of contemporary Texas Hill Country wines: Austin Formation (a fine red), Ste. Genevieve (a table white), and Los Alamos (a hearty pink Zinfandel). The raw materials, labor, and contribution per case of each of these wines is summarized below.
Grapes Variety A bushels Grapes Variety B bushels Sugar pounds Labor (man- hours) Contrib. per case Austin Formation 4 0 1 3 \ 24 Ste. Genevieve 0 4 0 1 \ 28 Los Alamos 2 2 2 2 \ 20
The winery has 2800 bushels of Variety A grapes, 2040 bushels of Variety B grapes, 800 pounds of sugar, and 1060 man-hours of labor available during the next week. The firm operates to achieve maximum contribution. Refer to the POM for Windows panels showing the solution to this problem.
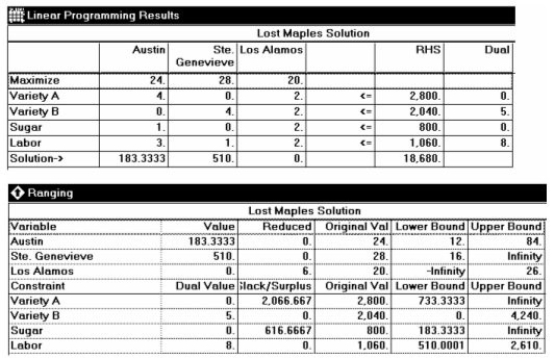 Answer the following questions.
a. For maximum contribution, how much of each wine should be produced?
b. How much contribution will be made by selling the output?
c. Is there any sugar left over?
If so, how much?
If not, what is its shadow price (dual value)?
Explain what this value means to Lost Maples' management.
d. Interpret the meaning of the lower bound to Labor in the Ranging analysis. That is, explain how the solution would change if the amount of labor fell below that lower value.
e. Interpret the meaning of the upper bound to Los Alamos wine in the Ranging analysis.
Answer the following questions.
a. For maximum contribution, how much of each wine should be produced?
b. How much contribution will be made by selling the output?
c. Is there any sugar left over?
If so, how much?
If not, what is its shadow price (dual value)?
Explain what this value means to Lost Maples' management.
d. Interpret the meaning of the lower bound to Labor in the Ranging analysis. That is, explain how the solution would change if the amount of labor fell below that lower value.
e. Interpret the meaning of the upper bound to Los Alamos wine in the Ranging analysis.
(Essay)
4.8/5  (34)
(34)
A linear programming problem has two constraints 2X + 4Y = 100 and 1X + 8Y ≤ 100, plus non-negativity constraints on X and Y. Which of the following statements about its feasible region is true?
(Multiple Choice)
4.9/5  (39)
(39)
Suppose that the shadow price for assembly time is $5/hour. If all assembly hours were used under the initial LP solution and workers normally make $4/hour but can work overtime for $6/hour, what should management do?
(Multiple Choice)
4.9/5  (34)
(34)
John's Locomotive Works manufactures a model locomotive. It comes in two versions--a standard (X1), and a deluxe (X2). The standard version generates $250 per locomotive for the standard version, and $350 per locomotive for the deluxe version. One constraint on John's production is labor hours. He only has 40 hours per week for assembly. The standard version requires 250 minutes each, while the deluxe requires 350 minutes. John's milling machine is also a limitation. There are only 20 hours a week available for the milling machine. The standard unit requires 60 minutes, while the deluxe requires 120. Formulate as a linear programming problem, and solve using either the graphical or corner points solution method.
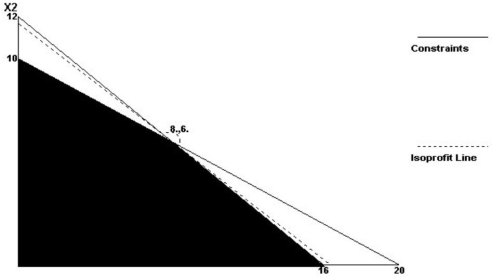
(Essay)
4.9/5  (33)
(33)
What combination of a and b will yield the optimum for this problem?
Maximize $6a + $15b, subject to (1) 4a + 2b < 12 and (2) 5a + 2b < 20 and (3) a, b ≥ 0.
(Multiple Choice)
4.8/5  (37)
(37)
In sensitivity analysis, a zero shadow price (or dual value) for a resource ordinarily means that the resource has not been used up.
(True/False)
4.9/5  (28)
(28)
The difference between minimization and maximization problems is that
(Multiple Choice)
4.8/5  (34)
(34)
Suppose that a constraint is given by X+Y≤10. If another constraint is given to be 3X+2Y≥15 determine the corners of the feasible solution. If the profit from X is 5 and the profit from Y is 10, determine the maximum profit.
(Essay)
4.9/5  (41)
(41)
A linear programming problem has two constraints 2X + 4Y ≤ 100 and 1X + 8Y ≤ 100, plus nonnegativity constraints on X and Y. Which of the following statements about its feasible region is true?
(Multiple Choice)
4.8/5  (27)
(27)
In a linear programming problem, what is the relationship between the constraints and the feasible region?
Explain with reference to a problem with two variables.
(Essay)
4.9/5  (42)
(42)
What combination of x and y will yield the optimum for this problem?
Maximize $3x + $15y, subject to (1) 2x + 4y < 12 and (2) 5x + 2y < 10 and (3) x, y ≥ 0.
(Multiple Choice)
4.9/5  (31)
(31)
Which of the following correctly describes all iso-profit lines for an LP maximization problem?
(Multiple Choice)
4.8/5  (32)
(32)
Suppose that a maximization LP problem has corners of (0,0), (10,0), (5,5), and (0,7). If profit is given to be X+ 2Y what is the maximum profit the company can earn?
(Multiple Choice)
4.8/5  (37)
(37)
The __________ is the set of all feasible combinations of the decision variables.
(Short Answer)
4.9/5  (33)
(33)
A stereo mail order center has 8,000 cubic feet available for storage of its private label loudspeakers. The ZAR-3 speakers cost $295 each and require 4 cubic feet of space; the ZAR-2ax speakers cost $110 each and require 3 cubic feet of space; and the ZAR-4 model costs $58 and requires 1 cubic foot of space. The demand for the ZAR-3 is at most 20 units per month. The wholesaler has $100,000 to spend on loudspeakers this month. Each ZAR-3 contributes $105, each ZAR-2ax contributes $50, and each ZAR-4 contributes $28. The objective is to maximize total contribution. Write out the objective and the constraints.
(Essay)
4.9/5  (43)
(43)
A financial advisor is about to build an investment portfolio for a client who has $100,000 to invest. The four investments available are A, B, C, and D. Investment A will earn 4 percent and has a risk of two "points" per $1,000 invested. B earns 6 percent with 3 risk points; C earns 9 percent with 7 risk points; and D earns 11 percent with a risk of 8. The client has put the following conditions on the investments: A is to be no more than one-half of the total invested. A cannot be less than 20 percent of the total investment. D cannot be less than C. Total risk points must be at or below 1,000.Identify the decision variables of this problem. Write out the objective function and constraints. Do not solve.
(Essay)
4.9/5  (30)
(30)
Two methods of conducting sensitivity analysis on solved linear programming problems are __________ and __________.
(Short Answer)
4.8/5  (35)
(35)
Showing 21 - 40 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)