Exam 9: Techniques of Integration
Exam 1: The Derivative189 Questions
Exam 2: Applications of the Derivative93 Questions
Exam 3: Techniques of Differentiation69 Questions
Exam 4: Logarithm Functions135 Questions
Exam 5: Applications of the Exponential and Natural Logarithm Functions73 Questions
Exam 6: The Definite Integral135 Questions
Exam 7: Functions of Several Variables119 Questions
Exam 8: The Trigonometric Functions128 Questions
Exam 9: Techniques of Integration178 Questions
Exam 10: Differential Equations126 Questions
Exam 11: Taylor Polynomials and Infinite Series132 Questions
Exam 12: Probability and Calculus92 Questions
Select questions type
Determine the integral by making an appropriate substitution.
-
(Multiple Choice)
4.8/5  (35)
(35)
The shaded area in the diagram represents an estimation dx using: 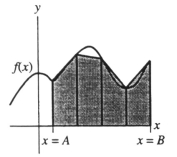
(Multiple Choice)
4.8/5  (39)
(39)
Approximate dx; n = 4, by (a) Simpson's rule and (b) the trapezoidal rule.
Enter your answers in that order as just unlabeled real numbers rounded to two decimal places, separated by a comma.
(Short Answer)
4.9/5  (36)
(36)
Determine the integral by making an appropriate substitution.
- dθ
(Multiple Choice)
4.9/5  (28)
(28)
Determine the integral by making an appropriate substitution.
-
(Multiple Choice)
4.7/5  (40)
(40)
Enter your answer with any coefficients in front as integers or reduced fractions of form a/b.
(Short Answer)
4.8/5  (37)
(37)
A company estimates that the rate of revenue produced by an investment will be K(t) thousand dollars per year at time t, where Find the present value of this stream of income over the next four years using 10% interest rate.
Enter just an integer (no units) representing the amount to the nearest dollar.
(Short Answer)
4.9/5  (36)
(36)
Evaluate the improper integral whenever it is convergent. If it is divergent, state this.
-
(Multiple Choice)
4.9/5  (40)
(40)
Approximate the integral by the trapezoidal rule.
- dx; n = 4 Express your answer to four decimal places.
(Multiple Choice)
4.9/5  (43)
(43)
Approximate dx; n = 6, by (a) Simpson's rule and (b) the trapezoidal rule.
Enter your answers in that order as just unlabeled real numbers rounded to two decimal places, separated by a comma.
(Short Answer)
4.9/5  (47)
(47)
Enter your answer with any coefficients in front as integers or reduced fractions of form . No parentheses around arguments of functions.
(Short Answer)
4.9/5  (51)
(51)
Showing 81 - 100 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)