Exam 11: Experimental Design and Analysis of Variance
Exam 1: An Introduction to Business Statistics54 Questions
Exam 2: Descriptive Statistics: Tabular and Graphical Methods90 Questions
Exam 3: Descriptive Statistics: Numerical Methods149 Questions
Exam 4: Probability135 Questions
Exam 5: Discrete Random Variables128 Questions
Exam 6: Continuous Random Variables150 Questions
Exam 7: Sampling and Sampling Distributions116 Questions
Exam 8: Confidence Intervals144 Questions
Exam 9: Hypothesis Testing148 Questions
Exam 10: Statistical Inferences Based on Two Samples132 Questions
Exam 11: Experimental Design and Analysis of Variance115 Questions
Exam 12: Chi-Square Tests96 Questions
Exam 13: Simple Linear Regression Analysis148 Questions
Exam 14: Multiple Regression122 Questions
Exam 15: Model Building and Model Diagnostics102 Questions
Exam 16: Time Series Forecasting150 Questions
Exam 17: Process Improvement Using Control Charts122 Questions
Exam 18: Nonparametric Methods97 Questions
Exam 19: Decision Theory90 Questions
Select questions type
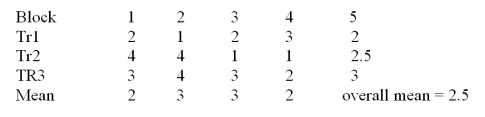 Consider the randomized block design with 4 blocks and 3 treatments given above. What are the degrees of freedom for blocks?
Consider the randomized block design with 4 blocks and 3 treatments given above. What are the degrees of freedom for blocks?
(Multiple Choice)
4.8/5  (37)
(37)
In one-way ANOVA,the numerator degrees of freedom equals the number of samples being compared.
(True/False)
4.7/5  (36)
(36)
If the total sum of squares in a one-way analysis of variance is 25 and the treatment sum of squares is 17,then the error sum of squares is?
(Multiple Choice)
4.8/5  (32)
(32)
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments.  What is the treatment mean square?
What is the treatment mean square?
(Multiple Choice)
4.8/5  (31)
(31)
 Consider the randomized block design with 4 blocks and 3 treatments given above. What are the degrees of freedom for treatments?
Consider the randomized block design with 4 blocks and 3 treatments given above. What are the degrees of freedom for treatments?
(Multiple Choice)
4.8/5  (34)
(34)
 Consider the randomized block design with 4 blocks and 3 treatments given above. What is the total sum of squares?
Consider the randomized block design with 4 blocks and 3 treatments given above. What is the total sum of squares?
(Multiple Choice)
4.8/5  (40)
(40)
Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations. MSE = 101.25 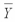 overall = 39
overall = 39 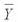 1 = 33
1 = 33 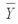 2 = 43
2 = 43 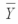 3 = 49
3 = 49 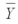 4 = 31
Compute a 95% confidence interval for the first treatment mean.
4 = 31
Compute a 95% confidence interval for the first treatment mean.
(Multiple Choice)
4.8/5  (30)
(30)
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments.  What is the calculated F statistic for treatments?
What is the calculated F statistic for treatments?
(Multiple Choice)
4.7/5  (25)
(25)
Experimental data is collected so that the values of the dependent variables are set before the values of the independent variable are observed.
(True/False)
4.8/5  (28)
(28)
The degrees of freedom treatment (between group variation)of a completely randomized design (one-way)ANOVA test with 4 groups and 15 observations per each group is:
(Multiple Choice)
4.7/5  (33)
(33)
 Consider the randomized block design with 4 blocks and 3 treatments given above. What is the value of the F statistic for blocks?
Consider the randomized block design with 4 blocks and 3 treatments given above. What is the value of the F statistic for blocks?
(Multiple Choice)
4.8/5  (38)
(38)
 Consider the randomized block design with 4 blocks and 3 treatments given above. What is the treatment sum of squares?
Consider the randomized block design with 4 blocks and 3 treatments given above. What is the treatment sum of squares?
(Multiple Choice)
4.7/5  (25)
(25)
A researcher has used a one-way analysis of variance model to test whether the average starting salaries differ among the recent graduates from nursing,engineering,business and education disciplines.She has randomly selected four graduates from each of the four areas. If MSE = 4,and SSTO = 120 complete the following ANOVA table and determine the value of the F statistic. 
(Multiple Choice)
4.9/5  (36)
(36)
 Consider the randomized block design with 4 blocks and 3 treatments given above. What is the treatment mean square?
Consider the randomized block design with 4 blocks and 3 treatments given above. What is the treatment mean square?
(Multiple Choice)
4.9/5  (26)
(26)
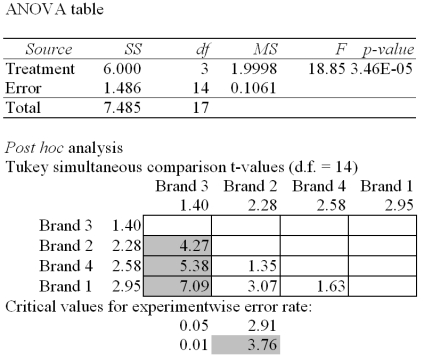 The Excel/Mega-Stat output given above summarizes the results of a one-way analysis of variance in an attempt to compare the performance characteristics of four brands of vacuum cleaners.The response variable is the amount of time it takes to clean a specific size room with a specific amount of dirt. At a significance level of .05,we would:
The Excel/Mega-Stat output given above summarizes the results of a one-way analysis of variance in an attempt to compare the performance characteristics of four brands of vacuum cleaners.The response variable is the amount of time it takes to clean a specific size room with a specific amount of dirt. At a significance level of .05,we would:
(Multiple Choice)
4.9/5  (38)
(38)
Consider the one-way ANOVA table.  What is the treatment mean square?
What is the treatment mean square?
(Multiple Choice)
4.8/5  (33)
(33)
The dependent variable,the variable of interest in an experiment,is also called ___________ variable.
(Multiple Choice)
4.7/5  (24)
(24)
In one-way ANOVA,as the between-treatment variation decreases,the probability of rejecting the null hypothesis increases.
(True/False)
4.9/5  (33)
(33)
In performing a one-way ANOVA,the _________ is the between group variance.
(Multiple Choice)
4.8/5  (26)
(26)
Showing 21 - 40 of 115
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)