Exam 15: Multiple Integrals
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
The joint density function for random variables 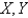 and
and 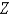 is
is 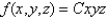 for
for 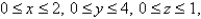 and
and 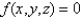 otherwise. Find the value of the constant
otherwise. Find the value of the constant  .
Round the answer to the nearest thousandth.
.
Round the answer to the nearest thousandth.
(Essay)
4.9/5  (36)
(36)
Use the Midpoint Rule for double integrals with 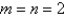 to estimate the area of the surface. Round your answer to three decimal places.
to estimate the area of the surface. Round your answer to three decimal places. 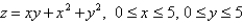
(Short Answer)
4.9/5  (34)
(34)
Find the mass of the lamina that occupies the region 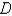 and has the given density function. Round your answer to two decimal places.
and has the given density function. Round your answer to two decimal places. 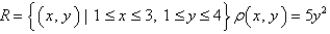
(Essay)
4.8/5  (44)
(44)
A cylindrical drill with radius 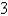 is used to bore a hole through the center of a sphere of radius
is used to bore a hole through the center of a sphere of radius 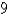 . Find the volume of the ring-shaped solid that remains. Round the answer to the nearest hundredth.
. Find the volume of the ring-shaped solid that remains. Round the answer to the nearest hundredth.
(Essay)
4.7/5  (35)
(35)
Use the given transformation to evaluate the integral. 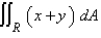 , where R is the square with vertices (0, 0), (4, 6), (6,
, where R is the square with vertices (0, 0), (4, 6), (6, 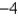 ), (10, 2) and
), (10, 2) and 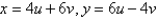
(Multiple Choice)
4.8/5  (27)
(27)
Find the volume of the solid bounded by the surface 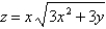 and the planes
and the planes 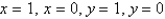 , and
, and 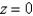 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Essay)
4.7/5  (30)
(30)
Evaluate the iterated integral 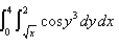 by reversing the order of integration.
by reversing the order of integration.
(Essay)
4.8/5  (30)
(30)
Use spherical coordinates to find the volume of the solid that lies within the sphere 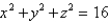 above the xy-plane and below the cone
above the xy-plane and below the cone 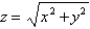 . Round the answer to two decimal places.
. Round the answer to two decimal places.
(Short Answer)
4.9/5  (39)
(39)
Find the volume of the given solid.
Under the paraboloid 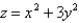 and above the rectangle
and above the rectangle 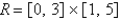 .
.
(Essay)
4.9/5  (29)
(29)
Find the area of the surface S where S is the part of the sphere 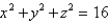 that lies to the right of the xz-plane and inside the cylinder
that lies to the right of the xz-plane and inside the cylinder 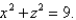
(Essay)
4.8/5  (33)
(33)
A lamina occupies the part of the disk 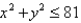 in the first quadrant. Find its center of mass if the density at any point is proportional to its distance from the x-axis.
in the first quadrant. Find its center of mass if the density at any point is proportional to its distance from the x-axis.
(Essay)
4.8/5  (36)
(36)
Find the area of the part of the plane 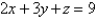 that lies inside the cylinder
that lies inside the cylinder 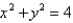 .
.
(Essay)
4.7/5  (38)
(38)
Determine whether to use polar coordinates or rectangular coordinates to evaluate the integral 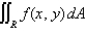 , where f is a continuous function. Then write an expression for the (iterated) integral.
, where f is a continuous function. Then write an expression for the (iterated) integral. 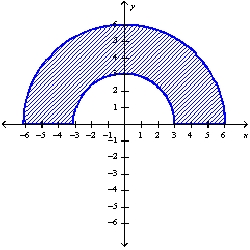
(Essay)
4.8/5  (28)
(28)
Find the center of mass of the lamina of the region shown if the density of the circular lamina is four times that of the rectangular lamina. 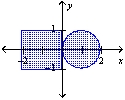
(Essay)
4.7/5  (38)
(38)
Evaluate the double integral by first identifying it as the volume of a solid. 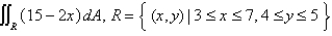
(Multiple Choice)
4.8/5  (33)
(33)
Find the moment of inertia about the y-axis for a cube of constant density 3 and side length 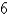 if one vertex is located at the origin and three edges lie along the coordinate axes.
if one vertex is located at the origin and three edges lie along the coordinate axes.
(Essay)
4.8/5  (38)
(38)
Use the transformation 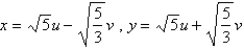 to evaluate the integral
to evaluate the integral 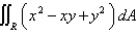 , where R is the region bounded by the ellipse
, where R is the region bounded by the ellipse 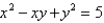 .
.
(Multiple Choice)
4.9/5  (35)
(35)
Find the center of mass of the lamina that occupies the region D and has the given density function, if D is bounded by the parabola 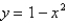 and the x-axis.
and the x-axis. 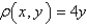
(Multiple Choice)
4.9/5  (37)
(37)
Showing 41 - 60 of 124
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)