Exam 15: Multiple Integrals
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Find the area of the surface S where S is the part of the plane 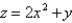 that lies above the triangular region with vertices
that lies above the triangular region with vertices 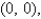
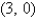 , and
, and 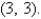
(Essay)
4.9/5  (34)
(34)
Use cylindrical coordinates to evaluate the triple integral 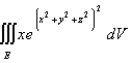 where E is the solid that lies between the sphere
where E is the solid that lies between the sphere 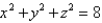 and
and 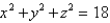 in the first octant.
in the first octant.
(Essay)
4.8/5  (34)
(34)
Use a computer algebra system to find the moment of inertia 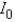 of the lamina that occupies the region D and has the density function
of the lamina that occupies the region D and has the density function 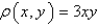 , if
, if 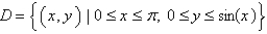 .
.
(Multiple Choice)
4.8/5  (33)
(33)
The sketch of the solid is given below. Given 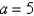 , write the inequalities that describe it.
, write the inequalities that describe it. 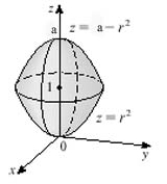
(Multiple Choice)
4.8/5  (40)
(40)
Evaluate the integral 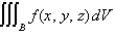 where
where 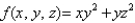 and
and 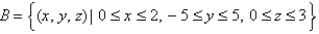 with respect to x, y, and z, in that order.
with respect to x, y, and z, in that order.
(Multiple Choice)
4.8/5  (30)
(30)
Find the area of the part of hyperbolic paraboloid 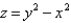 that lies between the cylinders
that lies between the cylinders 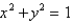 and
and 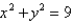 .
.
(Multiple Choice)
4.9/5  (34)
(34)
Evaluate the double integral 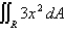 , where
, where 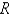 is the region bounded by the graphs of
is the region bounded by the graphs of 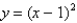 and
and 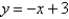 .
.
(Essay)
4.8/5  (35)
(35)
Compute 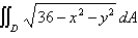 , where
, where 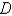 is the disk
is the disk 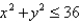 , by first identifying the integral as the volume of a solid.
, by first identifying the integral as the volume of a solid.
(Essay)
4.9/5  (33)
(33)
Express the volume of the wedge in the first octant that is cut from the cylinder 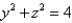 by the planes
by the planes 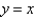 and
and 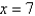 as an iterated integral with respect to
as an iterated integral with respect to 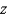 , then to
, then to 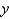 , then to
, then to 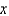 .
.
(Essay)
4.8/5  (36)
(36)
Find the area of the surface S where S is the part of the surface 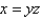 that lies inside the cylinder
that lies inside the cylinder 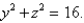
(Essay)
4.9/5  (40)
(40)
Find the moment of inertia with respect to a diameter of the base of a solid hemisphere of radius 3 with constant mass density function 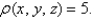
(Essay)
4.8/5  (36)
(36)
Find the mass of the solid S bounded by the paraboloid 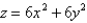 and the plane
and the plane 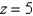 if S has constant density 3.
if S has constant density 3.
(Multiple Choice)
4.8/5  (39)
(39)
Set up, but do not evaluate, the iterated integral giving the mass of the solid T bounded by the cylinder 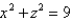 in the first octant and the plane
in the first octant and the plane 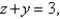 having mass density given by
having mass density given by 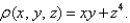
(Essay)
4.9/5  (29)
(29)
Find the area of the surface S where S is the part of the sphere 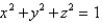 that lies inside the cylinder
that lies inside the cylinder 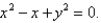
(Essay)
4.8/5  (33)
(33)
An agricultural sprinkler distributes water in a circular pattern of radius 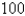 ft. It supplies water to a depth of
ft. It supplies water to a depth of 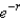 feet per hour at a distance of
feet per hour at a distance of 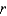 feet from the sprinkler. What is the total amount of water supplied per hour to the region inside the circle of radius
feet from the sprinkler. What is the total amount of water supplied per hour to the region inside the circle of radius 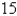 feet centered at the sprinkler?
feet centered at the sprinkler?
(Essay)
5.0/5  (30)
(30)
Evaluate the iterated integral by converting to polar coordinates. Round the answer to two decimal places. 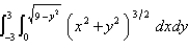 .
.
(Multiple Choice)
4.9/5  (37)
(37)
Showing 61 - 80 of 124
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)