Exam 5: Applications of Integration
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
In a steam engine the pressure and volume of steam satisfy the equation 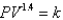 , where k is a constant. (This is true for adiabatic expansion, that is, expansion in which there is no heat transfer between the cylinder and its surroundings.) Calculate the work done by the engine (in ft-lb) during a cycle when the steam starts at a pressure of
, where k is a constant. (This is true for adiabatic expansion, that is, expansion in which there is no heat transfer between the cylinder and its surroundings.) Calculate the work done by the engine (in ft-lb) during a cycle when the steam starts at a pressure of 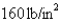 and a volume of
and a volume of 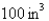 and expands to a volume of
and expands to a volume of 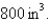 Use the fact that the work done by the gas when the volume expands from
Use the fact that the work done by the gas when the volume expands from 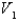 to volume
to volume 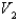 is
is 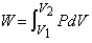 .
.
(Essay)
5.0/5  (43)
(43)
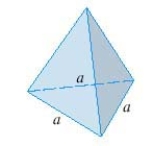
Find the volume of a pyramid with height 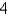 and base an equilateral triangle with side a =
and base an equilateral triangle with side a = 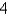 .
. 
(Multiple Choice)
4.7/5  (35)
(35)
The base of S is a circular region with boundary curve 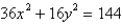 . Cross-sections perpendicular to the x axis are isosceles right triangles with hypotenuse in the base.
Find the volume of S.
. Cross-sections perpendicular to the x axis are isosceles right triangles with hypotenuse in the base.
Find the volume of S.
(Essay)
4.9/5  (32)
(32)
Set up, but do not evaluate, an integral for the volume of the solid obtained by rotating the region bounded by the given curves about the specified axis. 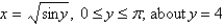
(Essay)
5.0/5  (29)
(29)
BiFind the number b such that the line 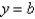 divides the region bounded by the curves
divides the region bounded by the curves 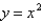 and
and 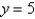 into two regions with equal area.
into two regions with equal area.
(Multiple Choice)
4.8/5  (39)
(39)
Use cylindrical shells to find the volume of the solid. A sphere of radius 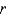 .
.
(Multiple Choice)
4.8/5  (30)
(30)
Find the volume common to two spheres, each with radius r = 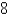 if the center of each sphere lies on the surface of the other sphere.
if the center of each sphere lies on the surface of the other sphere.
(Essay)
4.8/5  (31)
(31)
The base of a solid is a circular disk with radius 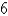 . Find the volume of the solid if parallel cross-sections perpendicular to the base are isosceles right triangles with hypotenuse lying along the base.
. Find the volume of the solid if parallel cross-sections perpendicular to the base are isosceles right triangles with hypotenuse lying along the base.
(Essay)
4.9/5  (32)
(32)
Find the area of the region bounded by the graph of f (x) = 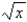 , the y-axis, and the tangent line to the graph of f at (16, 4).
, the y-axis, and the tangent line to the graph of f at (16, 4).
(Short Answer)
4.8/5  (40)
(40)
In a certain city the temperature 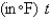 hours after 7 A.M. was modeled by the function
hours after 7 A.M. was modeled by the function 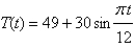 Find the average temperature to three decimal places during the period from 7 A.M. to 7 P.M.
Find the average temperature to three decimal places during the period from 7 A.M. to 7 P.M.
(Essay)
4.8/5  (40)
(40)
Use the Midpoint Rule with n = 4 to estimate the volume obtained by rotating about the region under the y-axis the region under the curve. 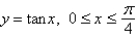 The choices are rounded to the nearest hundredth.
The choices are rounded to the nearest hundredth.
(Multiple Choice)
4.8/5  (47)
(47)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis.
y = x2, y = 0, x = 3, x = 5; the x-axis
(Essay)
4.8/5  (40)
(40)
Sketch a graph to estimate the x-coordinates of the points of intersection of the given curves. Then use this information to estimate the volume of the solid obtained by rotating about the y axis the region enclosed by these curves. Rounded to the nearest hundredth. 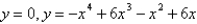
(Multiple Choice)
4.9/5  (41)
(41)
Showing 81 - 100 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)