Exam 5: Applications of Integration
Exam 1: Functions and Limits117 Questions
Exam 2: Derivatives151 Questions
Exam 3: Applications of Differentiation153 Questions
Exam 4: Integrals95 Questions
Exam 5: Applications of Integration120 Questions
Exam 6: Inverse Functions127 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration86 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates72 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
The height of a monument is 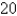 m. A horizontal cross-section at a distance x meters from the top is an equilateral triangle with side
m. A horizontal cross-section at a distance x meters from the top is an equilateral triangle with side 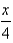 meters. Find the volume of the monument.
meters. Find the volume of the monument.
(Multiple Choice)
4.7/5  (37)
(37)
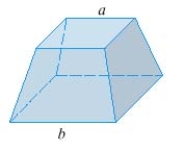
The volume of the frustum of a pyramid with square base of side b = 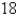 , square top of side a =
, square top of side a = 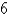 , and height h =
, and height h = 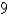 is
is  .
. 
(True/False)
4.7/5  (42)
(42)
Find the volume of the solid obtained by rotating the region bounded by 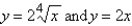 about the line
about the line 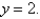
(Multiple Choice)
4.8/5  (40)
(40)
Use the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle.
y = 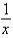 , y = 0, x = 2, x = 5; the y-axis
, y = 0, x = 2, x = 5; the y-axis
(Essay)
4.9/5  (32)
(32)
Use the method of cylindrical shells to find the volume of the solid generated by revolving the region bounded by the graphs of the equations about the indicated axis. Sketch the region and a representative rectangle.
y = 3x2, y = 0, x = 1; the y-axis
(Essay)
4.9/5  (31)
(31)
The base of a solid is the region bounded by the graphs of y = 4 - x2 and y = 0. The cross sections perpendicular to the y-axis are equilateral triangles. Find the volume of the solid.
(Essay)
4.8/5  (32)
(32)
Use the method of cylindrical shells to find the volume of solid obtained by rotating the region bounded by the given curves about the x-axis. 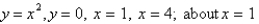
(Multiple Choice)
4.9/5  (26)
(26)
Use a graphing utility to (a) plot the graphs of the given functions and (b) find the x-coordinates of the points of intersection of the curves. Then find an approximation of the area of the region bounded by the curves using the integration capabilities of the graphing utility. Round answers to two decimal places.
y = 3x2, y = 5 - x4
(Essay)
4.8/5  (41)
(41)
The velocity v of blood that flows in a blood vessel with radius 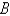 and length l at a distance
and length l at a distance 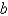 from the central axis is
from the central axis is 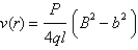 where P is the pressure difference between the ends of the vessel and q is the viscosity of the blood. Find the average velocity (with respect to r) over the interval
where P is the pressure difference between the ends of the vessel and q is the viscosity of the blood. Find the average velocity (with respect to r) over the interval 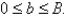
(Essay)
4.9/5  (39)
(39)
The tank shown is full of water. Given that water weighs 62.5 lb/ft and R = 5, find the work (in lb-ft) required to pump the water out of the tank. 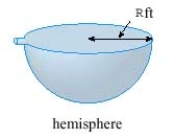
(Short Answer)
4.9/5  (41)
(41)
Find the volume of the solid generated by revolving the region bounded by the graphs of the equations and inequalities about the y-axis. x2 - y2 = 36, x 0, y = -6, y = 6
(Multiple Choice)
4.9/5  (42)
(42)
Sketch a plane region, and indicate the axis about which it is revolved so that the resulting solid of revolution has the volume given by the integral. 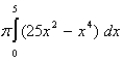
(Essay)
4.8/5  (31)
(31)
Use the graph of f shown in the figure to evaluate the integral by interpreting it geometrically. 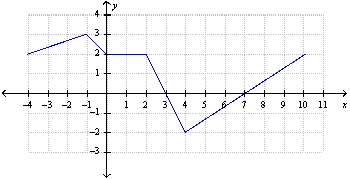
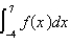
(Multiple Choice)
4.8/5  (47)
(47)
A tank is full of water. Find the work required to pump the water out of the outlet. 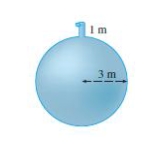
(Multiple Choice)
4.8/5  (42)
(42)
If 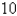 J of work are needed to stretch a spring from
J of work are needed to stretch a spring from 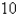 cm to
cm to 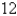 cm and another
cm and another 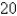 J are needed to stretch it from
J are needed to stretch it from 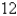 cm to
cm to 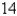 cm, what is the natural length of the spring? Round the answer to nearest integer.
cm, what is the natural length of the spring? Round the answer to nearest integer.
(Multiple Choice)
4.8/5  (35)
(35)
If 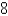 J of work are needed to stretch a spring from 8 cm to 14 cm and another
J of work are needed to stretch a spring from 8 cm to 14 cm and another 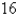 J are needed to stretch it from 14 cm to 19 cm, what is the natural length of the spring?
J are needed to stretch it from 14 cm to 19 cm, what is the natural length of the spring?
(Essay)
4.8/5  (39)
(39)
The temperature of a metal rod, 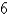 m long, is
m long, is 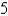 x (in degree Celsius) at a distance x meters from one end of the rod. What is the average temperature of the rod?
x (in degree Celsius) at a distance x meters from one end of the rod. What is the average temperature of the rod?
(Multiple Choice)
4.8/5  (41)
(41)
The height of a monument is 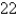 m. A horizontal cross-section at a distance x meters from the top is an equilateral triangle with side x/4 meters. Find the volume of the monument.
m. A horizontal cross-section at a distance x meters from the top is an equilateral triangle with side x/4 meters. Find the volume of the monument.
(Essay)
4.8/5  (45)
(45)
Showing 101 - 120 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)