Question 1

Evaluate the integral using an appropriate trigonometric substitution. $\int_{1}^{4} \frac{\sqrt{x^{2}-1}}{x^{4}} d x$

Accepted Answer

The answer of Evaluate the integral using an appropriate trigonometric...

Question 2

A body moves along a coordinate line in such a way that its velocity at any time t, where $0 \leq t \leq 6$ , is given by $v(t)=t \sqrt{36-t^{2}}$ .
Find its position function if it is initially located at the origin.

Accepted Answer

The answer of A body moves along a coordinate line...

Question 3

Find the integral. $\int \frac{d x}{x(x-2)}$

Accepted Answer

A)  $2 \ln \left|\frac{x^{2}-2}{x}\right|+C$ 
B)  $2 \ln \left|\frac{x-2}{x}\right|+C$ 
C)  $\frac{1}{2} \ln \left|\frac{x^{2}-2}{x}\right|+C$ 
D)  $\frac{1}{2} \ln \left|\frac{x-2}{x}\right|+C$ 
A)  $2 \ln \left|\frac{x^{2}-2}{x}\right|+C$ 
B)  $2 \ln \left|\frac{x-2}{x}\right|+C$ 
C)  $\frac{1}{2} \ln \left|\frac{x^{2}-2}{x}\right|+C$ 
D)  $\frac{1}{2} \ln \left|\frac{x-2}{x}\right|+C$

Question 4

Find the integral. $\int \frac{x^{3}-3 x^{2}+6 x-2}{x^{3}-2 x^{2}+x} d x$

Accepted Answer

A)  $\ln \left|\frac{x-1}{x^{2}}\right|-\frac{1}{x-1}+x+C$ 
B)  $\ln \left|\frac{x^{2}}{x-1}\right|-\frac{2}{x-1}+x+C$ 
C)  $\ln \left|\frac{x-1}{x^{2}}\right|-\frac{2}{x-1}+x+C$ 
D)  $\ln \left|\frac{x^{2}}{x-1}\right|-\frac{1}{x-1}+x+C$ 
A)  $\ln \left|\frac{x-1}{x^{2}}\right|-\frac{1}{x-1}+x+C$ 
B)  $\ln \left|\frac{x^{2}}{x-1}\right|-\frac{2}{x-1}+x+C$ 
C)  $\ln \left|\frac{x-1}{x^{2}}\right|-\frac{2}{x-1}+x+C$ 
D)  $\ln \left|\frac{x^{2}}{x-1}\right|-\frac{1}{x-1}+x+C$

Question 5

Use a table of integrals to evaluate the integral. $\int x \sqrt{2+2 x} d x$

Accepted Answer

A)  $\frac{2 \sqrt{2}}{15}(2 x-1)(x+1)^{3 / 2}+C$ 
B)  $\frac{2 \sqrt{2}}{15}(3 x-2)(x+1)^{3 / 2}+C$ 
C)  $\frac{2}{15}(3 x-2) \sqrt{x+1}+C$ 
D)  $\frac{2 \sqrt{2}}{15}(3 x-2) \sqrt{x+1}+C$ 
A)  $\frac{2 \sqrt{2}}{15}(2 x-1)(x+1)^{3 / 2}+C$ 
B)  $\frac{2 \sqrt{2}}{15}(3 x-2)(x+1)^{3 / 2}+C$ 
C)  $\frac{2}{15}(3 x-2) \sqrt{x+1}+C$ 
D)  $\frac{2 \sqrt{2}}{15}(3 x-2) \sqrt{x+1}+C$

Question 6

Use a table of integrals to evaluate the integral. $\int e^{-7 x} \sin 3 x d x$

Accepted Answer

A)  $-\frac{1}{10} e^{-7 x}(7 \sin 3 x+7 \cos 3 x)+C$ 
B)  $-\frac{1}{10} e^{-7 x}(7 \sin 3 x+3 \cos 3 x)+C$ 
C)  $-\frac{1}{58} e^{-7 x}(7 \sin 3 x+7 \cos 3 x)+C$ 
D)  $-\frac{1}{58} e^{-7 x}(7 \sin 3 x+3 \cos 3 x)+C$ 
A)  $-\frac{1}{10} e^{-7 x}(7 \sin 3 x+7 \cos 3 x)+C$ 
B)  $-\frac{1}{10} e^{-7 x}(7 \sin 3 x+3 \cos 3 x)+C$ 
C)  $-\frac{1}{58} e^{-7 x}(7 \sin 3 x+7 \cos 3 x)+C$ 
D)  $-\frac{1}{58} e^{-7 x}(7 \sin 3 x+3 \cos 3 x)+C$

Question 7

Determine whether the improper integral converges or diverges, and if it converges, find its value. $\int_{2}^{\infty} \frac{d x}{x \sqrt{x^{2}-4}}$

Accepted Answer

The answer of Determine whether the improper integral converges or...

Question 8

Find the integral. $\int x e^{3 x} d x$

Accepted Answer

A)  $\frac{1}{3}(3 x-1) e^{3 x}+C$ 
B)  $\frac{1}{9}(3 x-1) e^{3 x}+C$ 
C)  $\frac{1}{6} x^{2} e^{3 x}+C$ 
D)  $\frac{1}{4} x e^{4 x}+C$ 
A)  $\frac{1}{3}(3 x-1) e^{3 x}+C$ 
B)  $\frac{1}{9}(3 x-1) e^{3 x}+C$ 
C)  $\frac{1}{6} x^{2} e^{3 x}+C$ 
D)  $\frac{1}{4} x e^{4 x}+C$

Question 9

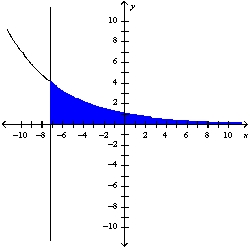
The region $\left\{(x+y) \mid x \geq-7,0 \leq y \leq e^{-x / 5}\right\}$ is represented below. Find the area of this region to two decimal places.

Accepted Answer

A)  20.28 
B)  $17.89$ 
C)  $16.08$ 
D)  $15.89$ 
E)  $15.87$ 
A)  20.28 
B)  $17.89$ 
C)  $16.08$ 
D)  $15.89$ 
E)  $15.87$

Question 10

A manufacturer of light bulbs wants to produce bulbs that last about $400$ hours but, of course, some bulbs burn out faster than others. Let $F(t)$ be the fraction of the company's bulbs that burn out before t hours. $F(t)$ lies between 0 and 1. Let $r(t)=F^{\prime}(t)$ . What is the value of $\int_{0}^{\infty} r(t) d t$ ?

Accepted Answer

A)  $\int_{0}^{\infty} r(t) d t=400$ 
B)  $\int_{0}^{\infty} r(t) d t=2$ 
C)  $\int_{0}^{\infty} r(t) d t=0$ 
D)  $\text { divergent }$ 
E)  $\int_{0}^{\infty} r(t) d t=1$ 
A)  $\int_{0}^{\infty} r(t) d t=400$ 
B)  $\int_{0}^{\infty} r(t) d t=2$ 
C)  $\int_{0}^{\infty} r(t) d t=0$ 
D)  $\text { divergent }$ 
E)  $\int_{0}^{\infty} r(t) d t=1$

Question 11

Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. $ \int_{1}^{4} \sqrt{x} d x ; \quad n=5 $

Accepted Answer

The answer of Find a bound on the error in...

Question 12

Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. $\int_{-3}^{6} x^{3} d x ; \quad n=6$

Accepted Answer

The answer of Find a bound on the error in...

Question 13

Find the integral. $\int \cot ^{2} x \csc ^{6} x d x$

Accepted Answer

The answer of Find the integral. \(\int \cot ^{2} x...

Question 14

Find the integral. $\int \frac{x^{3}+4 x+7}{(x+1)\left(x^{2}+1\right)} d x$

Accepted Answer

The answer of Find the integral. \(\int \frac{x^{3}+4 x+7}{(x+1)\left(x^{2}+1\right)} d...

Question 15

Evaluate the integral. $\int \frac{1}{\sqrt{x+2}+(x+2) \sqrt{x+2}} d x$

Accepted Answer

The answer of Evaluate the integral. \(\int \frac{1}{\sqrt{x+2}+(x+2) \sqrt{x+2}} d...

Question 16

Eight milligrams of a dye are injected into a vein leading the an individual's heart. The concentration of dye in the aorta (in milligrams per liter) measured at 2-sec intervals is shown in the accompanying table. Use Simpson's Rule with $n=12$ and the formula $R=\frac{60 D}{\int_{0}^{24} C(t) d t}$ to estimate the person's cardiac output, where D is the quantity of dye injected in milligrams, C(t)  is the concentration of the dye in the aorta, and R is measured in liters per minute. Round to one decimal place.
$\begin{array}{|l|c|c|c|c|c|c|c|c|c|c|c|c|c|}
\hline t & 0 & 2 & 4 & 6 & 8 & 10 & 12 & 14 & 16 & 18 & 20 & 22 & 24 \
\hline C(t) & 0 & 0 & 2.6 & 5.9 & 9.7 & 7.9 & 4.6 & 3.5 & 2.2 & 0.8 & 0.2 & 0.1 & 0 \
\hline
\end{array}$

Accepted Answer

6.5 liters

Question 17

Evaluate the integral. $\int e^{t} \sqrt{25-e^{2 t}} d t$

Accepted Answer

A)  $25 \arcsin \left(\frac{e^{t}}{5}\right)+\frac{1}{2} \sqrt{25-e^{2 t}}+C$ 
B)  $\frac{25}{2} \arcsin \left(\frac{e^{2 t}}{5}\right)+\frac{1}{2} \sqrt{5-e^{2}}+C$ 
C)  $\arcsin \left(\frac{e^{t}}{5}\right)+25 e^{t} \sqrt{25-e^{2 t}}+C$ 
D)  $\arcsin \left(\frac{e^{t}}{5}\right)-\frac{1}{2} \sqrt{25-e^{2 t}}+C$ 
E)  $\frac{25}{2}$ $\arcsin \left(\frac{e^{t}}{5}\right)+\frac{1}{2} e^{t} \sqrt{25-e^{2 t}}+C$ 
A)  $25 \arcsin \left(\frac{e^{t}}{5}\right)+\frac{1}{2} \sqrt{25-e^{2 t}}+C$ 
B)  $\frac{25}{2} \arcsin \left(\frac{e^{2 t}}{5}\right)+\frac{1}{2} \sqrt{5-e^{2}}+C$ 
C)  $\arcsin \left(\frac{e^{t}}{5}\right)+25 e^{t} \sqrt{25-e^{2 t}}+C$ 
D)  $\arcsin \left(\frac{e^{t}}{5}\right)-\frac{1}{2} \sqrt{25-e^{2 t}}+C$ 
E)  $\frac{25}{2}$ $\arcsin \left(\frac{e^{t}}{5}\right)+\frac{1}{2} e^{t} \sqrt{25-e^{2 t}}+C$

Question 18

Find the average value of the function $f(x)$ in the interval $[-\pi, \pi]$ . $f(x)=\sin ^{6} x \cos ^{5} x$

Accepted Answer

A)  $\pi$ 
B)  0 
C)  $\frac{\pi}{5}$ 
D)  $\frac{\pi}{12}$ 
E)  $\frac{\pi}{6}$ 
A)  $\pi$ 
B)  0 
C)  $\frac{\pi}{5}$ 
D)  $\frac{\pi}{12}$ 
E)  $\frac{\pi}{6}$

Question 19

Evaluate the integral. $\int_{0}^{8}\left(x^{2}+8\right) e^{-x} d x$

Accepted Answer

A)  $30 e^{-4}+10$ 
B)  $-30 e^{4}+10$ 
C)  $-90 e^{-8}+10$ 
D)  $-30 e^{-4}-1$ 
E)  $\text { None of these }$ 
A)  $30 e^{-4}+10$ 
B)  $-30 e^{4}+10$ 
C)  $-90 e^{-8}+10$ 
D)  $-30 e^{-4}-1$ 
E)  $\text { None of these }$

Question 20

Use the Table of Integrals to evaluate the integral. $\int \frac{x^{2}}{\sqrt{x^{6}-6}} d x$

Accepted Answer

The answer of Use the Table of Integrals to evaluate...

Evaluate the integral using an appropriate trigonometric substitution. $\int_{1}^{4} \frac{\sqrt{x^{2}-1}}{x^{4}} d x$

A body moves along a coordinate line in such a way that its velocity at any time t, where $0 \leq t \leq 6$ , is given by $v(t)=t \sqrt{36-t^{2}}$ . Find its position function if it is initially located at the origin.

Find the integral. $\int \frac{d x}{x(x-2)}$

Find the integral. $\int \frac{x^{3}-3 x^{2}+6 x-2}{x^{3}-2 x^{2}+x} d x$

Use a table of integrals to evaluate the integral. $\int x \sqrt{2+2 x} d x$

Use a table of integrals to evaluate the integral. $\int e^{-7 x} \sin 3 x d x$

Determine whether the improper integral converges or diverges, and if it converges, find its value. $\int_{2}^{\infty} \frac{d x}{x \sqrt{x^{2}-4}}$

Find the integral. $\int x e^{3 x} d x$

The region $\left\{(x+y) \mid x \geq-7,0 \leq y \leq e^{-x / 5}\right\}$ is represented below. Find the area of this region to two decimal places. $The region \left\{(x+y) \mid x \geq-7,0 \leq y \leq e^{-x / 5}\right\} is represented below. Find the area of this region to two decimal places.$

Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. $\int_{1}^{4} \sqrt{x} d x ; \quad n=5$

Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. $\int_{-3}^{6} x^{3} d x ; \quad n=6$

Find the integral. $\int \cot ^{2} x \csc ^{6} x d x$

Find the integral. $\int \frac{x^{3}+4 x+7}{(x+1)\left(x^{2}+1\right)} d x$

Evaluate the integral. $\int \frac{1}{\sqrt{x+2}+(x+2) \sqrt{x+2}} d x$

Evaluate the integral. $\int e^{t} \sqrt{25-e^{2 t}} d t$

Find the average value of the function $f(x)$ in the interval $[-\pi, \pi]$ . $f(x)=\sin ^{6} x \cos ^{5} x$

Evaluate the integral. $\int_{0}^{8}\left(x^{2}+8\right) e^{-x} d x$

Use the Table of Integrals to evaluate the integral. $\int \frac{x^{2}}{\sqrt{x^{6}-6}} d x$

Functions and Limits

Derivatives

Applications of Differentiation

Integrals

Applications of Integration

Inverse Functions

Further Applications of Integration

Differential Equations

Parametric Equations and Polar Coordinates

Infinite Sequences and Series

Vectors and the Geometry of Space

Vector Functions

Partial Derivatives

Multiple Integrals

Vector Calculus

Second-Order Differential Equations

Final Exam

Filters

Exam 7: Techniques of Integration

Evaluate the integral using an appropriate trigonometric substitution. ∫14x2−1x4dx\int_{1}^{4} \frac{\sqrt{x^{2}-1}}{x^{4}} d x∫14​x4x2−1​​dx

A body moves along a coordinate line in such a way that its velocity at any time t, where 0≤t≤60 \leq t \leq 60≤t≤6 , is given by v(t)=t36−t2v(t)=t \sqrt{36-t^{2}}v(t)=t36−t2​ . Find its position function if it is initially located at the origin.

Find the integral. ∫dxx(x−2)\int \frac{d x}{x(x-2)}∫x(x−2)dx​

Find the integral. ∫x3−3x2+6x−2x3−2x2+xdx\int \frac{x^{3}-3 x^{2}+6 x-2}{x^{3}-2 x^{2}+x} d x∫x3−2x2+xx3−3x2+6x−2​dx

Use a table of integrals to evaluate the integral. ∫x2+2xdx\int x \sqrt{2+2 x} d x∫x2+2x​dx

Use a table of integrals to evaluate the integral. ∫e−7xsin⁡3xdx\int e^{-7 x} \sin 3 x d x∫e−7xsin3xdx

Determine whether the improper integral converges or diverges, and if it converges, find its value. ∫2∞dxxx2−4\int_{2}^{\infty} \frac{d x}{x \sqrt{x^{2}-4}}∫2∞​xx2−4​dx​

Find the integral. ∫xe3xdx\int x e^{3 x} d x∫xe3xdx

The region {(x+y)∣x≥−7,0≤y≤e−x/5}\left\{(x+y) \mid x \geq-7,0 \leq y \leq e^{-x / 5}\right\}{(x+y)∣x≥−7,0≤y≤e−x/5} is represented below. Find the area of this region to two decimal places.

Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. ∫14xdx;n=5 \int_{1}^{4} \sqrt{x} d x ; \quad n=5 ∫14​x​dx;n=5

Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. ∫−36x3dx;n=6\int_{-3}^{6} x^{3} d x ; \quad n=6∫−36​x3dx;n=6

Find the integral. ∫cot⁡2xcsc⁡6xdx\int \cot ^{2} x \csc ^{6} x d x∫cot2xcsc6xdx

Find the integral. ∫x3+4x+7(x+1)(x2+1)dx\int \frac{x^{3}+4 x+7}{(x+1)\left(x^{2}+1\right)} d x∫(x+1)(x2+1)x3+4x+7​dx

Evaluate the integral. ∫1x+2+(x+2)x+2dx\int \frac{1}{\sqrt{x+2}+(x+2) \sqrt{x+2}} d x∫x+2​+(x+2)x+2​1​dx

Evaluate the integral. ∫et25−e2tdt\int e^{t} \sqrt{25-e^{2 t}} d t∫et25−e2t​dt

Find the average value of the function f(x)f(x)f(x) in the interval [−π,π][-\pi, \pi][−π,π] . f(x)=sin⁡6xcos⁡5xf(x)=\sin ^{6} x \cos ^{5} xf(x)=sin6xcos5x

Evaluate the integral. ∫08(x2+8)e−xdx\int_{0}^{8}\left(x^{2}+8\right) e^{-x} d x∫08​(x2+8)e−xdx

Use the Table of Integrals to evaluate the integral. ∫x2x6−6dx\int \frac{x^{2}}{\sqrt{x^{6}-6}} d x∫x6−6​x2​dx

Functions and Limits

Derivatives

Applications of Differentiation

Integrals

Applications of Integration

Inverse Functions

Further Applications of Integration

Differential Equations

Parametric Equations and Polar Coordinates

Infinite Sequences and Series

Vectors and the Geometry of Space

Vector Functions

Partial Derivatives

Multiple Integrals

Vector Calculus

Second-Order Differential Equations

Final Exam

Filters

Evaluate the integral using an appropriate trigonometric substitution. $\int_{1}^{4} \frac{\sqrt{x^{2}-1}}{x^{4}} d x$

A body moves along a coordinate line in such a way that its velocity at any time t, where $0 \leq t \leq 6$ , is given by $v(t)=t \sqrt{36-t^{2}}$ . Find its position function if it is initially located at the origin.

Find the integral. $\int \frac{d x}{x(x-2)}$

Find the integral. $\int \frac{x^{3}-3 x^{2}+6 x-2}{x^{3}-2 x^{2}+x} d x$

Use a table of integrals to evaluate the integral. $\int x \sqrt{2+2 x} d x$

Use a table of integrals to evaluate the integral. $\int e^{-7 x} \sin 3 x d x$

Determine whether the improper integral converges or diverges, and if it converges, find its value. $\int_{2}^{\infty} \frac{d x}{x \sqrt{x^{2}-4}}$

Find the integral. $\int x e^{3 x} d x$

The region $\left\{(x+y) \mid x \geq-7,0 \leq y \leq e^{-x / 5}\right\}$ is represented below. Find the area of this region to two decimal places. $The region \left\{(x+y) \mid x \geq-7,0 \leq y \leq e^{-x / 5}\right\} is represented below. Find the area of this region to two decimal places.$

Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. $\int_{1}^{4} \sqrt{x} d x ; \quad n=5$

Find a bound on the error in approximating the integral using (a) the Trapezoidal Rule and (b) Simpson's Rule with n subintervals. $\int_{-3}^{6} x^{3} d x ; \quad n=6$

Find the integral. $\int \cot ^{2} x \csc ^{6} x d x$

Find the integral. $\int \frac{x^{3}+4 x+7}{(x+1)\left(x^{2}+1\right)} d x$

Evaluate the integral. $\int \frac{1}{\sqrt{x+2}+(x+2) \sqrt{x+2}} d x$

Evaluate the integral. $\int e^{t} \sqrt{25-e^{2 t}} d t$

Find the average value of the function $f(x)$ in the interval $[-\pi, \pi]$ . $f(x)=\sin ^{6} x \cos ^{5} x$

Evaluate the integral. $\int_{0}^{8}\left(x^{2}+8\right) e^{-x} d x$

Use the Table of Integrals to evaluate the integral. $\int \frac{x^{2}}{\sqrt{x^{6}-6}} d x$