Exam 1: Functions and Limits
Exam 1: Functions and Limits95 Questions
Exam 2: Derivatives84 Questions
Exam 3: Applications of Differentiation155 Questions
Exam 4: Integrals169 Questions
Exam 5: Applications of Integration70 Questions
Exam 6: Inverse Functions95 Questions
Exam 7: Techniques of Integration124 Questions
Exam 8: Further Applications of Integration87 Questions
Exam 9: Differential Equations67 Questions
Exam 10: Parametric Equations and Polar Coordinates73 Questions
Exam 11: Infinite Sequences and Series158 Questions
Exam 12: Vectors and the Geometry of Space60 Questions
Exam 13: Vector Functions93 Questions
Exam 14: Partial Derivatives132 Questions
Exam 15: Multiple Integrals124 Questions
Exam 16: Vector Calculus137 Questions
Exam 17: Second-Order Differential Equations63 Questions
Exam 18: Final Exam44 Questions
Select questions type
Suppose that the graph of is drawn on a coordinate grid where the unit of measurement is an inch. How many miles to the right of the origin do we have to move before the height of the curve reaches 3 ft? Rounded to the nearest mile.
(Multiple Choice)
4.9/5  (31)
(31)
Determine whether the function whose graph is given is even, odd, or neither. 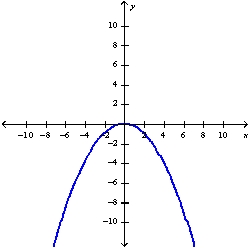
(Multiple Choice)
4.7/5  (36)
(36)
Find the inverse of
f. Then sketch the graphs of f and on the same set of axes.
f(x) = ,
(Short Answer)
4.8/5  (26)
(26)
Find the inverse of F) Then sketch the graphs of f and on the same set of axes. ,
(Multiple Choice)
4.7/5  (33)
(33)
An open rectangular box with volume 2 has a square base. Express the surface area of the box as a function of the length of a side of the base.
(Multiple Choice)
4.9/5  (45)
(45)
Starting with the graph of , write the equation of the graph that results from shifting 5 units right.
(Multiple Choice)
4.8/5  (31)
(31)
If a bacteria population starts with 100 bacteria and doubles every three hours, then the number of bacteria after t hours is . When will the population reach 35,000? Round the answer to the nearest tenth.
(Multiple Choice)
4.9/5  (37)
(37)
Find the points of intersection of the graphs of the functions. Express your answers accurate to five decimal places. f (x) = 0.5 - 1.7 + 2.3x - 2; = 2.8x - 4.8
(Multiple Choice)
4.8/5  (29)
(29)
A spherical balloon with radius inches has volume .
Find a function that represents the amount of air required to inflate the balloon from a radius of inches to a radius of inches.
(Short Answer)
4.9/5  (43)
(43)
By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box can be made. If the cardboard is 18 in. long and 9 in. wide and the square cutaways have dimensions of x in. by x in., find a function that gives the volume of the resulting box. 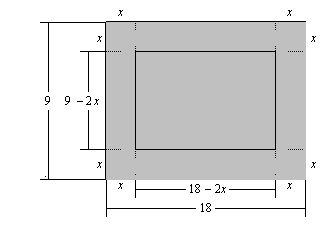
(Short Answer)
4.9/5  (38)
(38)
Scientists have discovered that a linear relationship exists between the amount of flobberworm mucus secretions and the air temperature. When the temperature is 65°F, the flobberworms each secrete 16 grams of mucus a day; when the temperature is 95°F, they each secrete 22 grams of mucus a day. Find a function M(t) that gives the amount of mucus secreted on a given day, where t is the temperature of that day in degrees Fahrenheit.
(Multiple Choice)
4.8/5  (34)
(34)
Showing 61 - 80 of 95
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)