Exam 18: Review of Statistical Inference
Exam 1: What Is Statistics39 Questions
Exam 2: Graphical and Tabular Descriptive Techniques192 Questions
Exam 3: Numerical Descriptive Techniques215 Questions
Exam 4: Data Collection and Sampling82 Questions
Exam 5: Probability200 Questions
Exam 6: Random Variables and Discrete Probability Distributions158 Questions
Exam 7: Continuous Probability Distributions149 Questions
Exam 8: Sampling Distributions127 Questions
Exam 9: Introduction to Estimation85 Questions
Exam 10: Introduction to Hypothesis Testing178 Questions
Exam 11: Inference About a Population75 Questions
Exam 12: Inference About Comparing Two Populations, Part 183 Questions
Exam 13: Inference About Comparing Two Populations, Part 284 Questions
Exam 14: Analysis of Variance125 Questions
Exam 15: Chi-Squared Tests118 Questions
Exam 16: Simple Linear Regression and Correlation231 Questions
Exam 17: Multiple Regression143 Questions
Exam 18: Review of Statistical Inference182 Questions
Select questions type
A regression analysis between weight (y in pounds) and height (x in inches) resulted in the following least squares line: 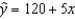 . This implies that if the height is increased by 1 inch, the weight, on average, is expected to:
. This implies that if the height is increased by 1 inch, the weight, on average, is expected to:
(Multiple Choice)
4.8/5  (41)
(41)
Two independent samples of sizes 20 and 30 are randomly selected from two normally distributed populations. Assume that the population variances are unknown but equal. In order to test the difference between the population means, 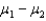 , the sampling distribution of the sample mean difference,
, the sampling distribution of the sample mean difference, 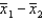 , is:
, is:
(Multiple Choice)
4.9/5  (33)
(33)
Five types of apples are displayed side by side in several supermarkets in the city of Miami. It was noted that in one day, 180 customers purchased apples. Of these, 30 picked type A, 40 picked type B, 25 picked type C, 35 picked type D, and 50 picked type E. In Miami, can you conclude at the 5% significance level that there is a preferred type of apples?
(Essay)
4.8/5  (41)
(41)
When testing 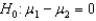 vs.
vs. 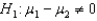 , the observed value of the z-score was found to be -2.15. Then, the p-value for this test would be
, the observed value of the z-score was found to be -2.15. Then, the p-value for this test would be
(Multiple Choice)
5.0/5  (28)
(28)
Multicollinearity affects the t-tests of the individual coefficients as well as the F-test in the analysis of variance for regression because the F-test combines the t-tests into a single test.
(True/False)
4.8/5  (38)
(38)
SSE stands for ____________________ of squares for ____________________.
(Short Answer)
4.8/5  (35)
(35)
The coefficient of ____________________ measures the amount of variation in the dependent variable that is explained by the variation in the independent variable.
(Short Answer)
4.9/5  (41)
(41)
Another name for the residual term in a regression equation is random error.
(True/False)
4.8/5  (34)
(34)
In testing the significance of a multiple regression model with three independent variables, the null hypothesis is 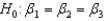 .
.
(True/False)
4.8/5  (31)
(31)
The degrees of freedom for the test statistic in a test of a contingency table is (r - 1)(c - 1) where r is the number of rows in the table, and c is the number of columns.
(True/False)
4.8/5  (44)
(44)
If we square the t-statistic for two means, the result is the ____________________-statistic.
(True/False)
4.9/5  (40)
(40)
The chi-squared goodness-of-fit test compares the ____________________ frequencies in the table to the ____________________ frequencies based on the null hypothesis.
(Short Answer)
4.9/5  (35)
(35)
Consider a multinomial experiment involving 100 trials and 3 categories (cells). The observed frequencies resulting from the experiment are shown in the accompanying table.
 Use the 5% significance level to test the hypotheses H0: p1 = 0.45, p2 = 0.30, p3 = 0.25 vs. H1: At least two proportions differ from their specified values.
Use the 5% significance level to test the hypotheses H0: p1 = 0.45, p2 = 0.30, p3 = 0.25 vs. H1: At least two proportions differ from their specified values.
(Essay)
4.9/5  (36)
(36)
In testing for the differences between the means of two independent populations where the variances in each population are unknown but assumed equal, the degrees of freedom is:
(Multiple Choice)
4.8/5  (40)
(40)
The test statistic used to test hypotheses about the population variance is given by 2 = (n -1)s2 / 2, which is chi-squared distributed with n - 1 degrees of freedom when the population is normally distributed with variance equal to 2.
(True/False)
4.9/5  (39)
(39)
In testing for the equality of two population variances, when the populations are normally distributed, the 10% level of significance has been used. To determine the rejection region, it will be necessary to refer to the F table corresponding to an upper-tail area of:
(Multiple Choice)
4.8/5  (39)
(39)
In a matched pairs experiment the parameter of interest is the ____________________ of the population of ____________________.
(Short Answer)
4.8/5  (39)
(39)
The alternative hypothesis of ANOVA is that ____________________ population means are different.
(Short Answer)
4.9/5  (35)
(35)
Multiple comparison methods are used to determine whether or not any differences occur amongst a group of population means.
(True/False)
4.7/5  (41)
(41)
Showing 141 - 160 of 182
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)