Exam 12: Inference About Comparing Two Populations, Part 1

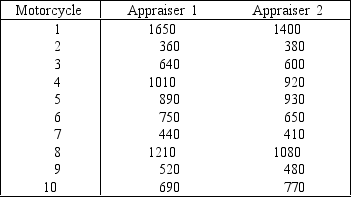
Motorcycle insurance appraisers examine motorcycles that have been involved in accidental collisions to assess the cost of repairs. An insurance executive is concerned that different appraisers produce significantly different assessments. In an experiment 10 motorcycles that have recently been involved in accidents were shown to two appraisers. Each assessed the estimated repair costs. These results are shown below. Can the executive conclude at the 5% significance level that the appraisers differ in their assessments?

Free

(Essay)

4.8/5

(36)

Question 1

Correct Answer:

Verified

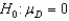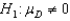, (Appraiser 1 - Appraiser 2)
Rejection region: | t | > t_0.025,9 = 2.262, Test statistic: t = 1.802
Conclusion: Don't reject the null hypothesis. The executive can't conclude at the 5% significance level that the appraisers differ in their assessments, according to this data.

Undergraduates' Test Scores: 35 undergraduate students who completed two years of college were asked to take a basic mathematics test. The mean and standard deviation of their scores were 75.1 and 12.8, respectively. In a random sample of 50 students who only completed high school, the mean and standard deviation of the test scores were 72.1 and 14.6, respectively -Estimate with 90% confidence the difference in mean scores between the two groups of students.

Free

(Essay)

4.8/5

(38)

Question 2

Correct Answer:

Verified

3.0 $\pm$ 4.98. Thus, LCL =-1.98, and UCL = 7.98.

Additives: A food processor wants to compare two additives for their effects on retarding spoilage. Suppose 16 cuts of fresh meat are treated with additive A and 16 are treated with additive B, and the number of hours until spoilage begins is recorded for each of the 32 cuts of meat. The results are summarized in the table below $Additives: A food processor wants to compare two additives for their effects on retarding spoilage. Suppose 16 cuts of fresh meat are treated with additive A and 16 are treated with additive B, and the number of hours until spoilage begins is recorded for each of the 32 cuts of meat. The results are summarized in the table below -Determine the rejection region at \alpha = .05 and write the proper conclusion.$ -Determine the rejection region at $\alpha$ = .05 and write the proper conclusion.

Free

(Essay)

4.8/5

(33)

Question 3

Correct Answer:

Verified

t < -t_.025,30 = -.042 or t > t_.025,30 = 2.042. Since t = 2.33 > 2.042, we reject the null hypothesis at $\alpha$ = .05 and conclude that the average number of hours until spoilage begins differs for additives A and B. Additive A helps the product last longer than Additive B, on average, according to this data.

The unequal-variances test statistic of 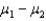has an approximate ____________________ distribution with n₁ + n₂- 2 degrees of freedom.

(Short Answer)

4.8/5

(41)

Question 4

Estimate with 95% confidence the difference between the two population means.

(Essay)

4.9/5

(35)

Question 5

The number of degrees of freedom associated with the t-test, when the data are gathered from a matched pairs experiment with 8 pairs, is 7.

(True/False)

4.9/5

(33)

Question 6

Two samples of sizes 25 and 20 are independently drawn from two normal populations, where the unknown population variances are assumed to be equal. The number of degrees of freedom of the equal-variances t-test statistic is 44.

(True/False)

4.7/5

(34)

Question 7

When we test for differences between the means of two independent populations, we can only use a two-tailed test.

(True/False)

4.9/5

(36)

Question 8

In testing the difference between two population means using two independent samples, we use the pooled variance in estimating the standard error of the sampling distribution of the sample mean difference 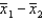if the populations are normal with equal variances.

(True/False)

4.9/5

(29)

Question 9

In comparing the difference in means with a matched pairs experiment, the variable under consideration is 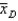, where the subscript D refers to the difference.

(True/False)

4.7/5

(38)

Question 10

Independent samples are those for which the selection process for one is not related to the selection process for the other.

(True/False)

4.8/5

(38)

Question 11

Clothing Expenditures: A marketing consultant was in the process of studying the perceptions of married couples concerning their monthly clothing expenditures. He believed that the husband's perception would be higher than the wife's. To judge his belief, he takes a random sample of ten married couples and asks each spouse to estimate the family clothing expenditure (in dollars) during the previous month. The data are shown below. 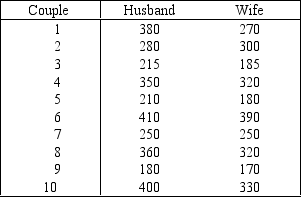-Briefly describe what the interval estimate tells you.

(Essay)

4.9/5

(27)

Question 12

The variance of is .

(True/False)

4.9/5

(34)

Question 13

A political analyst in Iowa surveys a random sample of registered Republicans and compares the results with those obtained from a random sample of registered Democrats . This would be an example of two independent samples.

(True/False)

4.8/5

(38)

Question 14

In a matched pairs experiment the parameter of interest is the of the population of .

(Short Answer)

4.8/5

(37)

Question 15

Aptitude Test Scores: Two random samples of 40 students were drawn independently from two populations of students. Assume their aptitude tests are normally distributed (total points = 100). The following statistics regarding their scores in an aptitude test were obtained: $Aptitude Test Scores: Two random samples of 40 students were drawn independently from two populations of students. Assume their aptitude tests are normally distributed (total points = 100). The following statistics regarding their scores in an aptitude test were obtained: 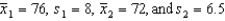. -Explain how to use the 95% confidence interval to test the hypotheses at \alpha = .05.$ . -Explain how to use the 95% confidence interval to test the hypotheses at $\alpha$ = .05.

(Essay)

4.9/5

(39)

Question 16

If we are testing for the difference between the means of two independent populations with equal variances, samples of n₁ = 15 and n₂ = 15 are taken, then the number of degrees of freedom is equal to

(Multiple Choice)

4.9/5

(30)

Question 17

The number of degrees of freedom associated with the t-test, when the data are gathered from a matched pairs experiment with 10 pairs, is:

(Multiple Choice)

4.8/5

(35)

Question 18

The quantity 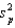is called the pooled variance estimate of the common variance of two unknown but equal population variances. It is the weighted average of the two sample variances, where the weights represent the:

(Multiple Choice)

4.9/5

(28)

Question 19

Promotional Campaigns: The general manager of a chain of fast food chicken restaurants wants to determine how effective their promotional campaigns are. In these campaigns "20% off" coupons are widely distributed. These coupons are only valid for one week. To examine their effectiveness, the executive records the daily gross sales (in $1,000s) in one restaurant during the campaign and during the week after the campaign ends. The data is shown below. 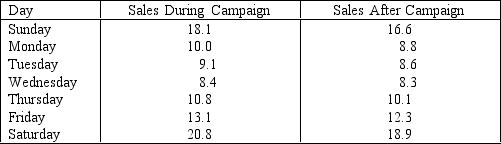-Estimate with 95% confidence the mean difference and interpret.

(Essay)

4.8/5

(38)

Question 20

Showing 1 - 20 of 83

The unequal-variances test statistic of has an approximate ____________________ distribution with n₁ + n₂- 2 degrees of freedom.

Estimate with 95% confidence the difference between the two population means.

The number of degrees of freedom associated with the t-test, when the data are gathered from a matched pairs experiment with 8 pairs, is 7.

Two samples of sizes 25 and 20 are independently drawn from two normal populations, where the unknown population variances are assumed to be equal. The number of degrees of freedom of the equal-variances t-test statistic is 44.

When we test for differences between the means of two independent populations, we can only use a two-tailed test.

In testing the difference between two population means using two independent samples, we use the pooled variance in estimating the standard error of the sampling distribution of the sample mean difference if the populations are normal with equal variances.

In comparing the difference in means with a matched pairs experiment, the variable under consideration is , where the subscript D refers to the difference.

Independent samples are those for which the selection process for one is not related to the selection process for the other.

The variance of is .

A political analyst in Iowa surveys a random sample of registered Republicans and compares the results with those obtained from a random sample of registered Democrats . This would be an example of two independent samples.

In a matched pairs experiment the parameter of interest is the of the population of .

If we are testing for the difference between the means of two independent populations with equal variances, samples of n₁ = 15 and n₂ = 15 are taken, then the number of degrees of freedom is equal to

The number of degrees of freedom associated with the t-test, when the data are gathered from a matched pairs experiment with 10 pairs, is:

The quantity is called the pooled variance estimate of the common variance of two unknown but equal population variances. It is the weighted average of the two sample variances, where the weights represent the:

What Is Statistics

Graphical and Tabular Descriptive Techniques

Numerical Descriptive Techniques

Data Collection and Sampling

Probability

Random Variables and Discrete Probability Distributions

Continuous Probability Distributions

Sampling Distributions

Introduction to Estimation

Introduction to Hypothesis Testing

Inference About a Population

Inference About Comparing Two Populations, Part 2

Analysis of Variance

Chi-Squared Tests

Simple Linear Regression and Correlation

Multiple Regression

Review of Statistical Inference

Filters

Exam 12: Inference About Comparing Two Populations, Part 1

The unequal-variances test statistic of has an approximate ____________________ distribution with n1 + n2- 2 degrees of freedom.

Estimate with 95% confidence the difference between the two population means.

The number of degrees of freedom associated with the t-test, when the data are gathered from a matched pairs experiment with 8 pairs, is 7.

Two samples of sizes 25 and 20 are independently drawn from two normal populations, where the unknown population variances are assumed to be equal. The number of degrees of freedom of the equal-variances t-test statistic is 44.

When we test for differences between the means of two independent populations, we can only use a two-tailed test.

In testing the difference between two population means using two independent samples, we use the pooled variance in estimating the standard error of the sampling distribution of the sample mean difference if the populations are normal with equal variances.

In comparing the difference in means with a matched pairs experiment, the variable under consideration is , where the subscript D refers to the difference.

Independent samples are those for which the selection process for one is not related to the selection process for the other.

The variance of is .

A political analyst in Iowa surveys a random sample of registered Republicans and compares the results with those obtained from a random sample of registered Democrats . This would be an example of two independent samples.

In a matched pairs experiment the parameter of interest is the ____________________ of the population of ____________________.

If we are testing for the difference between the means of two independent populations with equal variances, samples of n1 = 15 and n2 = 15 are taken, then the number of degrees of freedom is equal to

The number of degrees of freedom associated with the t-test, when the data are gathered from a matched pairs experiment with 10 pairs, is:

The quantity is called the pooled variance estimate of the common variance of two unknown but equal population variances. It is the weighted average of the two sample variances, where the weights represent the:

What Is Statistics

Graphical and Tabular Descriptive Techniques

Numerical Descriptive Techniques

Data Collection and Sampling

Probability

Random Variables and Discrete Probability Distributions

Continuous Probability Distributions

Sampling Distributions

Introduction to Estimation

Introduction to Hypothesis Testing

Inference About a Population

Inference About Comparing Two Populations, Part 2

Analysis of Variance

Chi-Squared Tests

Simple Linear Regression and Correlation

Multiple Regression

Review of Statistical Inference

Filters

The unequal-variances test statistic of has an approximate ____________________ distribution with n₁ + n₂- 2 degrees of freedom.

In a matched pairs experiment the parameter of interest is the of the population of .

If we are testing for the difference between the means of two independent populations with equal variances, samples of n₁ = 15 and n₂ = 15 are taken, then the number of degrees of freedom is equal to