Exam 11: Inference About a Population

A random sample of size 15 taken from a normally distributed population revealed a sample mean of 75 and a sample variance of 25. The upper limit of a 95% confidence interval for the population mean would equal:

A random sample is drawn from a normal distribution with mean $\mu$ and variance $\sigma$ ². The random variable (n -1)S² / $\sigma$ ² has a chi-squared probability distribution with n degrees of freedom.

If the sampled population is nonnormal, the t-test of the population mean $\mu$ is still valid, provided that the condition is not extreme.

Test the hypotheses at the 10% significance level.

Estimate the population variance with 90% confidence.

The test statistic used to test hypotheses about the population variance has a chi-squared distribution with ____________________ degrees of freedom.

When the population standard deviation is unknown and the population is ____________________, the test statistic for testing hypotheses about $\mu$ is the t-distribution with n - 1 degrees of freedom.

The test statistic to test hypotheses about the population variance has a chi-squared distribution with n - 1 degrees of freedom when the population random variable has a(n) ____________________ distribution.

When the population standard deviation is ____________________ and the population is normal, the test statistic for testing hypotheses about $\mu$ is the t-distribution with n - 1 degrees of freedom.

In order to interpret the p-value associated with hypothesis testing about the population mean $\mu$ , it is necessary to know the value of the test statistic.

Applicants' Grades: The grades of a sample of 10 applicants, selected at random from a large population, are 71, 86, 75, 63, 92, 70, 81, 59, 80, and 90. -Construct a 90% confidence interval estimate for the population standard deviation.

Does this data provide sufficient evidence at the 10% significance level to indicate that the manager is correct?

In forming a 95% confidence interval for a population mean from a sample size of 20, the number of degrees of freedom from the t-distribution equals 20.

The statistic 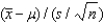when the sampled population is normal is Student t-distributed with n degrees of freedom.

What condition is required in order to analyze this data using a t-test?

Employees in a large company are entitled to 15-minute water breaks. A random sample of the duration of water breaks for 10 employees was taken with the times shown as: 12, 16, 14, 18, 21, 17, 19, 15, 18, and 16. Assuming that the times are normally distributed, is there enough evidence at the 5% significance level to indicate that on average employees are taking longer water breaks than they are entitled to?

When a population is small, we must adjust the test statistic and interval estimator using the ____________________ population correction factor.

Which of the following is not an example illustrating the use of variance?

During a natural gas shortage, a gas company randomly sampled residential gas meters in order to monitor daily gas consumption. On a particular day, a sample of 100 meters showed a sample mean of 250 cubic feet and a sample standard deviation of 50 cubic feet. Provide a 90% confidence interval estimate of the mean gas consumption for the population.

The chi-squared distribution can be used in constructing confidence intervals and carrying out hypothesis tests regarding the value of a population variance.