Exam 12: Inference About Comparing Two Populations, Part 1
Exam 1: What Is Statistics39 Questions
Exam 2: Graphical and Tabular Descriptive Techniques192 Questions
Exam 3: Numerical Descriptive Techniques215 Questions
Exam 4: Data Collection and Sampling82 Questions
Exam 5: Probability200 Questions
Exam 6: Random Variables and Discrete Probability Distributions158 Questions
Exam 7: Continuous Probability Distributions149 Questions
Exam 8: Sampling Distributions127 Questions
Exam 9: Introduction to Estimation85 Questions
Exam 10: Introduction to Hypothesis Testing178 Questions
Exam 11: Inference About a Population75 Questions
Exam 12: Inference About Comparing Two Populations, Part 183 Questions
Exam 13: Inference About Comparing Two Populations, Part 284 Questions
Exam 14: Analysis of Variance125 Questions
Exam 15: Chi-Squared Tests118 Questions
Exam 16: Simple Linear Regression and Correlation231 Questions
Exam 17: Multiple Regression143 Questions
Exam 18: Review of Statistical Inference182 Questions
Select questions type
Clothing Expenditures: A marketing consultant was in the process of studying the perceptions of married couples concerning their monthly clothing expenditures. He believed that the husband's perception would be higher than the wife's. To judge his belief, he takes a random sample of ten married couples and asks each spouse to estimate the family clothing expenditure (in dollars) during the previous month. The data are shown below.
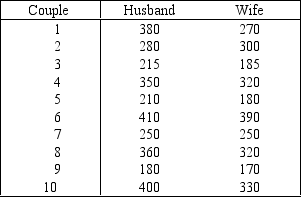 -Can the consultant conclude at the 5% significance level that the husband's estimate is higher than the wife's estimate?
-Can the consultant conclude at the 5% significance level that the husband's estimate is higher than the wife's estimate?
(Essay)
4.7/5  (39)
(39)
If there are 10 pairs of data in a matched pairs experiment, the degrees of freedom for the corresponding t-test is 18.
(True/False)
4.8/5  (25)
(25)
Two independent samples of sizes 20 and 30 are randomly selected from two normally distributed populations. Assume that the population variances are unknown but equal. In order to test the difference between the population means, 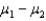 , the sampling distribution of the sample mean difference,
, the sampling distribution of the sample mean difference, 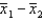 , is:
, is:
(Multiple Choice)
4.9/5  (36)
(36)
Explain how to use the 95% confidence interval to test the hypotheses at = .05.
(Essay)
4.8/5  (36)
(36)
Engine Wear: To compare the wearing of two types of automobile engines, 1 and 2, an experimenter chose to "pair" the measurements, comparing the wear for the two types of engines on each of 7 automobiles, as shown below.
 -Estimate with 90% confidence the mean difference and interpret.
-Estimate with 90% confidence the mean difference and interpret.
(Essay)
4.9/5  (28)
(28)
A behaviorist has performed the following experiment. For each of 10 sets of identical twins who were born 30 years ago, he recorded their annual incomes, according to which twin was born first. The results (in $1,000s) are shown below. Can he infer at 5% significance level that there is a difference in income between the twins?
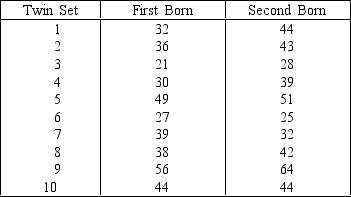
(Essay)
4.8/5  (34)
(34)
The equal-variances test statistic of 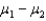 is Student t-distributed with n1 + n2 degrees of freedom, provided that the two populations are normal.
is Student t-distributed with n1 + n2 degrees of freedom, provided that the two populations are normal.
(True/False)
4.8/5  (36)
(36)
The pooled-variances t-test requires that the two population variances need not be the same.
(True/False)
4.9/5  (38)
(38)
When testing 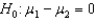 vs.
vs. 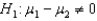 , the observed value of the z-score was found to be -2.15. Then, the p-value for this test would be
, the observed value of the z-score was found to be -2.15. Then, the p-value for this test would be
(Multiple Choice)
4.8/5  (31)
(31)
In constructing a confidence interval estimate for the difference between the means of two independent normally distributed populations, we:
(Multiple Choice)
4.8/5  (39)
(39)
Additives: A food processor wants to compare two additives for their effects on retarding spoilage. Suppose 16 cuts of fresh meat are treated with additive A and 16 are treated with additive B, and the number of hours until spoilage begins is recorded for each of the 32 cuts of meat. The results are summarized in the table below
 -Assume population variances are equal. Calculate the pooled variance and the value of the test statistic.
-Assume population variances are equal. Calculate the pooled variance and the value of the test statistic.
(Essay)
4.9/5  (35)
(35)
If some natural relationship exists between each pair of observations that provides a logical reason to compare the first observation of sample 1 with the first observation of sample 2, the second observation of sample 1 with the second observation of sample 2, and so on, the samples are referred to as:
(Multiple Choice)
4.9/5  (31)
(31)
The expected value of the difference of two sample means equals the difference of the corresponding population means when:
(Multiple Choice)
4.8/5  (34)
(34)
Engine Wear: To compare the wearing of two types of automobile engines, 1 and 2, an experimenter chose to "pair" the measurements, comparing the wear for the two types of engines on each of 7 automobiles, as shown below.
 -Determine whether these data are sufficient to infer at the 10% significance level that the two types of engines wear differently.
-Determine whether these data are sufficient to infer at the 10% significance level that the two types of engines wear differently.
(Essay)
4.9/5  (35)
(35)
Aptitude Test Scores: Two random samples of 40 students were drawn independently from two populations of students. Assume their aptitude tests are normally distributed (total points = 100). The following statistics regarding their scores in an aptitude test were obtained: 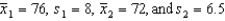 .
-Test at the 5% significance level to determine whether we can infer that the two population means differ.
.
-Test at the 5% significance level to determine whether we can infer that the two population means differ.
(Essay)
5.0/5  (32)
(32)
In testing for the differences between the means of two independent populations where the variances in each population are unknown but assumed equal, the degrees of freedom is:
(Multiple Choice)
4.9/5  (40)
(40)
Both the equal-variances and unequal variances test statistic and confidence interval estimator of 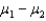 require that the two populations be normally distributed.
require that the two populations be normally distributed.
(True/False)
4.8/5  (29)
(29)
The best estimator of the difference between two population means 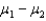 is the difference between two sample means
is the difference between two sample means 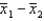 .
.
(True/False)
4.7/5  (32)
(32)
The test for the mean difference in a matched pairs design requires the differences to have a(n) ____________________ distribution.
(Short Answer)
4.8/5  (29)
(29)
Showing 41 - 60 of 83
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)