Exam 10: Introduction to Hypothesis Testing
Exam 1: What Is Statistics39 Questions
Exam 2: Graphical and Tabular Descriptive Techniques192 Questions
Exam 3: Numerical Descriptive Techniques215 Questions
Exam 4: Data Collection and Sampling82 Questions
Exam 5: Probability200 Questions
Exam 6: Random Variables and Discrete Probability Distributions158 Questions
Exam 7: Continuous Probability Distributions149 Questions
Exam 8: Sampling Distributions127 Questions
Exam 9: Introduction to Estimation85 Questions
Exam 10: Introduction to Hypothesis Testing178 Questions
Exam 11: Inference About a Population75 Questions
Exam 12: Inference About Comparing Two Populations, Part 183 Questions
Exam 13: Inference About Comparing Two Populations, Part 284 Questions
Exam 14: Analysis of Variance125 Questions
Exam 15: Chi-Squared Tests118 Questions
Exam 16: Simple Linear Regression and Correlation231 Questions
Exam 17: Multiple Regression143 Questions
Exam 18: Review of Statistical Inference182 Questions
Select questions type
For a given level of significance , if the sample size n is increased, the probability of a Type II error will:
(Multiple Choice)
5.0/5  (40)
(40)
If a sample size is increased at a given level, the probability of committing a Type II error is increased.
(True/False)
4.8/5  (44)
(44)
The critical values will bound the rejection and non-rejection regions for the null hypothesis.
(True/False)
4.9/5  (36)
(36)
Marathon Runners: A researcher wants to study the average miles run per day for marathon runners. In testing the hypotheses: H0: =25 miles vs. H1: 25 miles, a random sample of 36 marathon runners drawn from a normal population whose standard deviation is 10, produced a mean of 22.8 miles weekly.
-Develop a 95% confidence interval estimate of the population mean.
(Essay)
4.8/5  (28)
(28)
A Type II error is represented by ; it is the probability of rejecting a true null hypothesis.
(True/False)
4.7/5  (29)
(29)
If a researcher fails to reject a false null hypothesis he has made a(n) ____________________ error.
(Short Answer)
5.0/5  (32)
(32)
Watching the News: A researcher claims viewers spend an average of 40 minutes per day watching the news. You think the average is higher than that. In testing your hypotheses H0: = 40 vs. H1: F > 40, the following information came from your random sample of viewers: 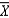 = 42 minutes, n = 25. Assume = 5.5, and = 0.10.
-Calculate the value of the test statistic.
= 42 minutes, n = 25. Assume = 5.5, and = 0.10.
-Calculate the value of the test statistic.
(Essay)
4.8/5  (32)
(32)
The ____________________ is a measure of the amount of statistical evidence that supports the alternative hypothesis.
(Short Answer)
4.7/5  (38)
(38)
LSAT Scores: The Admissions officer for the graduate programs at the University of Pennsylvania believes that the average score on the LSAT exam at his university is significantly higher than the national average of 1,300. An accepted standard deviation for LSAT scores is 125. A random sample of 25 scores had an average of 1,375.
-Use the p-value to test the hypotheses.
(Essay)
4.9/5  (46)
(46)
We have created a 95% confidence interval for with the result (8, 13). What conclusion will we make if we test H0: = 15 vs. H1: 15 at = 0.05?
(Multiple Choice)
4.8/5  (36)
(36)
Rechargeable Batteries: A researcher wants to study the average lifetime of a certain brand of rechargeable batteries (in hours). In testing the hypotheses, H0: = 950 hours vs. H1: 950 hours, a random sample of 25 rechargeable batteries is drawn from a normal population whose standard deviation is 200 hours.
-Calculate the power of the test when = 1000 and = 0.10.
(Essay)
4.9/5  (32)
(32)
To calculate the probability of a(n) ____________________ error you need to specify a value of other than the one given in the null hypothesis.
(Short Answer)
4.8/5  (31)
(31)
For a given level of significance, if the sample size is increased, the probability of committing a Type II error will decrease.
(True/False)
5.0/5  (35)
(35)
A sample is used to obtain a 95% confidence interval for the mean of a population. The confidence interval goes from 10.89 to 13.21. If the same sample had been used to test H0: F = 12 vs. H1: 12, H0 could not be rejected at the 0.05 level.
(True/False)
4.8/5  (43)
(43)
Watching the News: A researcher claims viewers spend an average of 40 minutes per day watching the news. You think the average is higher than that. In testing your hypotheses H0: = 40 vs. H1: F > 40, the following information came from your random sample of viewers: 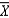 = 42 minutes, n = 25. Assume = 5.5, and = 0.10.
-Determine the p-value.
= 42 minutes, n = 25. Assume = 5.5, and = 0.10.
-Determine the p-value.
(Essay)
4.9/5  (34)
(34)
The p-value of a test is the probability of observing a test statistic at least as extreme as the one computed given that the null hypothesis is true.
(True/False)
4.9/5  (38)
(38)
Showing 41 - 60 of 178
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)