Exam 9: A: large-Sample Tests of Hypotheses
Exam 1: Describing Data With Graphs134 Questions
Exam 2: Describing Data With Numerical Measures235 Questions
Exam 3: Describing Bivariate Data57 Questions
Exam 4: A: probability and Probability Distributions107 Questions
Exam 4: B: probability and Probability Distributions157 Questions
Exam 5: Several Useful Discrete Distributions166 Questions
Exam 6: The Normal Probability Distribution235 Questions
Exam 7: Sampling Distributions231 Questions
Exam 8: Large-Sample Estimation187 Questions
Exam 9: A: large-Sample Tests of Hypotheses154 Questions
Exam 9: B: large-Sample Tests of Hypotheses106 Questions
Exam 10: A: Inference From Small Samples192 Questions
Exam 10: B: Inference From Small Samples124 Questions
Exam 11: A: The Analysis of Variance136 Questions
Exam 11: B: The Analysis of Variance137 Questions
Exam 12: A: linear Regression and Correlation131 Questions
Exam 12: B: linear Regression and Correlation171 Questions
Exam 13: Multiple Regression Analysis232 Questions
Exam 14: Analysis of Categorical Data158 Questions
Exam 15: A:nonparametric Statistics139 Questions
Exam 15: B:nonparametric Statistics95 Questions
Select questions type
In testing the difference between two population means using two independent samples, we use the pooled variance in estimating the standard error of the sampling distribution of the sample mean difference 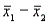 if the populations are normal with equal variances.
if the populations are normal with equal variances.
(True/False)
4.9/5  (42)
(42)
Which of the following would be an appropriate alternative hypothesis to test a proportion?
(Multiple Choice)
4.8/5  (37)
(37)
The probability of correctly accepting a true null hypothesis equals 1 - 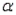 and is called the confidence level of the hypothesis test.
and is called the confidence level of the hypothesis test.
(True/False)
4.8/5  (42)
(42)
In testing the difference between two population means using two independent samples, the sampling distribution of the sample mean difference 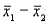 is normal if the sample sizes are both greater than 30.
is normal if the sample sizes are both greater than 30.
(True/False)
4.8/5  (35)
(35)
For testing the difference between two population proportions, under what circumstances should the pooled proportion estimate be used to compute the value of the test statistic?
(Multiple Choice)
4.8/5  (36)
(36)
If you wish to determine there is evidence that the average starting salary for finance graduates exceeds $42,000, how would you formulate the null and alternative hypotheses?
(Multiple Choice)
4.9/5  (29)
(29)
In estimating the difference between two population means, if a 90% confidence interval includes 0, then we can be 90% certain that the difference between the two population means is 0.
(True/False)
4.8/5  (26)
(26)
A two-tailed hypothesis test of the population mean is used when the alternative hypothesis takes the form 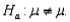
(True/False)
5.0/5  (29)
(29)
In testing 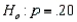 vs.
vs. 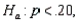 a random sample of size 200 produced a sample proportion
a random sample of size 200 produced a sample proportion 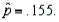 Given these results, the null hypothesis should not be rejected at
Given these results, the null hypothesis should not be rejected at 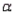 = 0.05.
= 0.05.
(True/False)
4.7/5  (41)
(41)
A hypothesis that specifies a range of values for the unknown parameter is called an interval estimate.
(True/False)
5.0/5  (39)
(39)
The campaign manager for the Conservatives believes that more than 52% of the registered voters will vote Conservative. If you wish to test this claim, the appropriate null and alternative hypotheses are 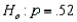 vs.
vs. 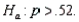
(True/False)
4.8/5  (38)
(38)
If the probability of committing a Type I error for a given test is to be decreased, then for a fixed sample size n, what will happen?
(Multiple Choice)
4.8/5  (33)
(33)
The upper limit of the 85% confidence interval for the population proportion p, given that n = 60 and 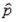 = 0.20, is 0.274.
= 0.20, is 0.274.
(True/False)
4.9/5  (36)
(36)
A Type II error for a statistical test is committed if we do not reject the null hypothesis when it is false.
(True/False)
4.7/5  (42)
(42)
Decision makers have more control over Type I error than Type II error.
(True/False)
4.8/5  (32)
(32)
The width of a confidence interval estimate for a proportion will be wider for a sample size of 100 than for a sample size of 50.
(True/False)
4.8/5  (36)
(36)
In a one-tailed test about the population proportion p, the p-value is found to be equal to 0.0352. If the test had been two-tailed, the p-value would have been 0.0704.
(True/False)
4.7/5  (31)
(31)
For a fixed sample size n, as the probability of a Type II error decreases, the probability of a Type I error increases.
(True/False)
4.9/5  (44)
(44)
Showing 41 - 60 of 154
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)