Exam 2: Describing Data With Numerical Measures

Two students are enrolled in different sections of an introductory statistics class at a local university. The first student, enrolled in the morning section, earns a score of 76 on a midterm exam where the class mean was 64 with a standard deviation of 8. The second student, enrolled in the afternoon section, earns a score of 72 on a midterm exam where the class mean was 60 with a standard deviation of 7.5. If the scores on the midterm exams are normally distributed, which student scored better relative to his or her classmates?

Athletic Training Time The following data represent the numbers of minutes an athlete spends training per day: 73, 74, 76, 77, 79, 79, 83, 84, 88, 84, 84, 85, 86, 86, 87, 87, 88, 91, 92, 92, 93, 97, 98, 98, 81, and 82. The mean and standard deviation were computed to be 85.54 and 6.97, respectively. -Refer to the Athletic Training Time statement. What percentage of the measurements lies in the interval (71.60, 99.48)?

Flu Shot Eight doctors were asked how many flu shots they had given to patients this fall. The numbers of flu shots were 6, 3, 5, 24, 2, 6, 0, and 8. -Refer to Flu Shot statement. Based on the values of the mean and median in the previous two questions, are the measurements symmetric or skewed? Why?

Measures of variability describe typical values in the data.

When the distribution is symmetric and unimodal, the mean = the median.

For any distribution, the standard deviation is a measure of the variability of the data around the median.

Calories in Soft Drinks The following data represent the number of calories in 340 mL cans of a sample of 8 popular soft drinks: 124, 144, 147, 146, 148, 154, 150, and 234. -Refer to the Calories in Soft Drinks statement. Find the median and the sample mean.

Athletic Training Time The following data represent the numbers of minutes an athlete spends training per day: 73, 74, 76, 77, 79, 79, 83, 84, 88, 84, 84, 85, 86, 86, 87, 87, 88, 91, 92, 92, 93, 97, 98, 98, 81, and 82. The mean and standard deviation were computed to be 85.54 and 6.97, respectively. -Refer to the Athletic Training Time statement. Create a stem-and-leaf plot for the distribution of training times.

The larger the values of the sample variance, 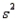, and the sample standard deviation, s, the greater the variability in the data.

The following 10 scores were obtained on a 20-point quiz: 4, 5, 8, 9, 11, 13, 15, 18, 18, and 20. The teacher computed the usual descriptive measures of centre and variability for these data, and then discovered an error was made. One of the 18s should have been a 16. Which pair of the following measures, calculated on the corrected data, would change from the original computation?

Motor Skills of Children The times required for 10 children to learn a particular motor skill were recorded as 9, 15, 23, 20, 16, 15, 24, 18, 10, and 20 minutes. -Refer to Motor Skills of Children statement. Based on the values of the mean and median in the previous two questions, are the measurements symmetric or skewed? Give a reason for your answer.

Parasites in Foxes A random sample of 100 foxes was examined by a team of veterinarians to determine the prevalence of a particular type of parasite. Counting the number of parasites per fox, the veterinarians found that 65 foxes had no parasites, 20 had one parasite, and so on. A frequency tabulation of the data is given here: -Refer to the Parasites in Foxes statement and table. Calculate the sample mean 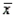and the sample standard deviation 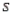for the sample.

A sample of 26 observations has a standard deviation of 4. What is the sum of the squared deviations from the sample mean?

Quartiles divide the values in a data set into four parts of equal size.

Solution Volumes An analytical chemist wanted to use electrolysis to determine the number of moles of cupric ions in a given volume of solution. The solution was partitioned into n = 30 portions of 0.2 mL each. Each of the n = 30 portions was tested. The average number of moles of cupric ions for the n = 30 portions was found to be 0.185 mole; the standard deviation was 0.015 mole. -Refer to the Solution Volumes statement. Describe the distribution of the measurements for the n = 30 portions of the solution using Tchebysheff's Theorem.

Frequency Table Suppose you are given the following frequency table of ratings from 0 to 8: 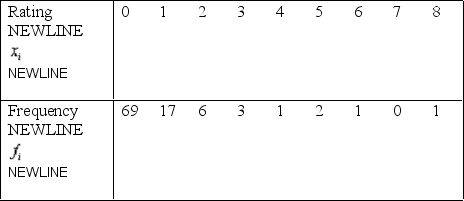Assume that the sample mean and the sample standard deviation are 0.66 and 1.387, respectively. -Refer to the Frequency Table Do the results of the previous question agree with the Empirical Rule?

Job Applicant Test Scores A new manufacturing plant has 20 job openings. To select the best 20 applicants from among the 1000 job seekers, the plant's personnel office administers a written aptitude test to all applicants. The average score on the aptitude test is 150 points, with a standard deviation of 10 points. Assume the distribution of test scores is approximately mound-shaped. -Refer to the Job Applicant Test Scores statement. What percentage of the test scores will fall between 130 and 160 points?

If a distribution is strongly skewed by one or more extreme values, you should use the mean rather than the median as a measure of centre.

Tchebysheff's Theorem states the following: Given a number k greater than or equal to 1, and a set of measurements, at least ( 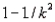) of the measurements in the data set will lie within k standard deviations of their mean.

Aptitude Tests Twenty-eight applicants interested in working in community services took an examination designed to measure their aptitude for social work. A stem-and-leaf plot of the 28 scores appears below, in which the first column is the count per "branch," the second column is the stem value, and the remaining digits are the leaves. Count Stems Leaves 1 4 6 1 5 9 4 6 3688 6 7 026799 9 8 145667788 7 9 1234788 -Refer to Aptitude Tests table. Use the range approximation to determine an approximate value for the standard deviation. Is this a good approximation?