Exam 12: Experimental Design and Analysis of Variance
Exam 1: An Introduction to Business Statistics and Analytics98 Questions
Exam 2: Descriptive Statistics and Analytics: Tabular and Graphical Methods120 Questions
Exam 3: Descriptive Statistics and Analytics: Numerical Methods145 Questions
Exam 4: Probability and Probability Models150 Questions
Exam 5: Predictive Analytics I: Trees, K-Nearest Neighbors, Naive Bayes,101 Questions
Exam 6: Discrete Random Variables150 Questions
Exam 7: Continuous Random Variables150 Questions
Exam 8: Sampling Distributions111 Questions
Exam 9: Confidence Intervals149 Questions
Exam 10: Hypothesis Testing150 Questions
Exam 11: Statistical Inferences Based on Two Samples140 Questions
Exam 12: Experimental Design and Analysis of Variance132 Questions
Exam 13: Chi-Square Tests120 Questions
Exam 14: Simple Linear Regression Analysis147 Questions
Exam 15: Multiple Regression and Model Building85 Questions
Exam 16: Predictive Analytics Ii: Logistic Regression, Discriminate Analysis,101 Questions
Exam 17: Time Series Forecasting and Index Numbers161 Questions
Exam 18: Nonparametric Methods103 Questions
Exam 19: Decision Theory90 Questions
Select questions type
The 95 percent individual confidence interval for μ1 − μ2 (treatment mean 1 − treatment mean 2) will always be smaller than the Tukey 95 percent simultaneous confidence interval for μ1 − μ2.
(True/False)
4.8/5  (29)
(29)
Consider the following partial analysis of variance table from a randomized block design with 10 blocks and 6 treatments.
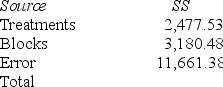 What is the mean square error?
What is the mean square error?
(Short Answer)
4.9/5  (30)
(30)
We have just performed a one-way ANOVA on a given set of data and rejected the null hypothesis for the ANOVA F test. Assume that we are able to perform a randomized block design ANOVA on the same data. For the randomized block design ANOVA, the null hypothesis for equal treatments will ________ be rejected.
(Multiple Choice)
4.9/5  (32)
(32)
A sum of squares that measures the variability among the sample means is referred to as the
(Multiple Choice)
4.8/5  (43)
(43)
 Consider the randomized block design with 4 blocks and 3 treatments given above. Test H0: there is no difference between blocks at α = .05.
Consider the randomized block design with 4 blocks and 3 treatments given above. Test H0: there is no difference between blocks at α = .05.
(Short Answer)
4.8/5  (37)
(37)
Consider a two-way analysis of variance experiment with treatment factors A and B. The results are summarized below.
 What are the levels of factor A and factor B?
What are the levels of factor A and factor B?
(Short Answer)
4.7/5  (39)
(39)
Which of the following is not an assumption for one-way analysis of variance?
(Multiple Choice)
4.9/5  (41)
(41)
A ________ design is an experimental design that compares v treatments by using d blocks, where each block is used exactly once to measure the effect of each treatment.
(Multiple Choice)
4.8/5  (32)
(32)
Consider a two-way analysis of variance experiment with treatment factors A and B, with factor A having four levels and factor B having three levels. The results are summarized below.
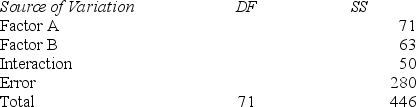 If there is an equal number of observations in each cell, what is the number of observations in each cell? (number of cells = level of factor A × level of factor
B)
If there is an equal number of observations in each cell, what is the number of observations in each cell? (number of cells = level of factor A × level of factor
B)
(Short Answer)
4.8/5  (44)
(44)
Suppose you are a researcher investigating the annual sales differences among five categories of businesses. The study looks at 55 companies equally divided among categories A, B, C, D, and E.
Determine degrees of freedom treatment, degrees of freedom error and degrees of freedom total and state the critical value of the F statistic at α = .05.
(Short Answer)
4.9/5  (30)
(30)
In one-way ANOVA, the numerator of the F statistic is an estimate of the population variance based on between-treatment variation.
(True/False)
4.9/5  (34)
(34)
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments.
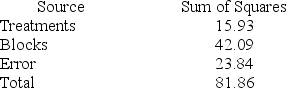 Test H0: There is no difference between blocks at α = .05.
Test H0: There is no difference between blocks at α = .05.
(Short Answer)
4.7/5  (31)
(31)
Consider a two-way analysis of variance experiment with treatment factors A and B, with factor A having four levels and factor B having three levels. The results are summarized below.
 Compute the mean squares and F to test the null hypothesis that no interaction exists between factor A and B at α = .05.
Compute the mean squares and F to test the null hypothesis that no interaction exists between factor A and B at α = .05.
(Short Answer)
4.9/5  (40)
(40)
Consider the following calculations for a one-way analysis of variance from a completely randomized design with 20 total observations equally divided into 4 treatments. The response variable is sales in millions of dollars and the four treatment levels represent the four regions that the company serves.
MSE = 101.25  = 39
= 39 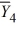 = 33
= 33 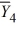 = 43
= 43 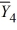 = 49
= 49 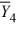 = 31
Perform a pairwise comparison between treatment mean 1 and treatment mean 4 by computing a Tukey 95 percent simultaneous confidence interval.
= 31
Perform a pairwise comparison between treatment mean 1 and treatment mean 4 by computing a Tukey 95 percent simultaneous confidence interval.
(Short Answer)
4.9/5  (29)
(29)
Interaction exists between two factors if the relationship between the mean response and one factor depends on the other factor.
(True/False)
4.7/5  (41)
(41)
In a one-way ANOVA table, the ________ the value of MSE, the higher the probability of rejecting the hypothesis that all treatment means are equal.
(Multiple Choice)
4.9/5  (34)
(34)
After rejecting the null hypothesis of equal treatments, a researcher decided to compute a 95 percent confidence interval for the difference between the mean of treatment 1 and mean of treatment 2 based on the Tukey procedure. At α = .05, if the confidence interval includes the value of zero, then we can reject the hypothesis that the two population means are equal.
(True/False)
4.9/5  (39)
(39)
Consider the following partial analysis of variance table from a randomized block design with 6 blocks and 4 treatments.
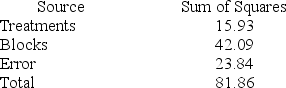 What is the mean square error?
What is the mean square error?
(Short Answer)
4.8/5  (31)
(31)
A vitamin-water manufacturer wants to compare the effects on sales of three water colors: green, blue, and red. Four regions are selected for the test, with the following ANOVA results.
 If there is no interaction effect, test the individual null hypotheses on the effect of each factor on mean sales at α = .01.
If there is no interaction effect, test the individual null hypotheses on the effect of each factor on mean sales at α = .01.
(Short Answer)
4.9/5  (39)
(39)
Showing 61 - 80 of 132
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)