Exam 7: Random Variables and Discrete Probability Distributions

The amount of milk consumed by a baby in a day is an example of a discrete random variable.

Katie's Portfolio Katie is given the following information about the returns on two stocks: E(R₁) = 0.10, E(R₂) = 0.15, V(R₁) = 0.0225, and V(R₂) = 0.0441. -{Katie's Portfolio Narrative} Compute the variance of the portfolio composed of 60% stock 1, and 40% stock 2, if the coefficient of correlation is 0.40.

Stress Consider a binomial random variable X with n = 5 and p = 0.40, where X represents the number of times in the final exam week a student with 18 credit hours may feel stressed. -{Stress Narrative} Find the expected number of times a student may feel stressed during the final exam week.

Katie's Portfolio Katie is given the following information about the returns on two stocks: E(R₁) = 0.10, E(R₂) = 0.15, V(R₁) = 0.0225, and V(R₂) = 0.0441. -{Katie's Portfolio Narrative} Compute the variance of the portfolio composed of 30% stock 1 and 70% stock 2, if the coefficient of correlation is 0.40.

Let X be a Poisson random variable with $\mu$ = 6.Use the table of Poisson probabilities to calculate: a. P(X $\le$ 8) b. P(X = 8) c. P(X $\ge$ 5) d. P(6 $\le$ X $\le$ 10)

Number of Hamsters The joint probability distribution of X and Y is shown in the accompanying table, where X denotes the number of hamsters that Quinn may have next year, and Y denotes the number of hamsters that her boyfriend, Jason, may have when she moves in with him next year. 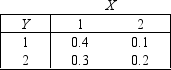-{Number of Hamsters Narrative} Determine the marginal probability distributions of X and Y.

If the probability of success p remains constant in a binomial distribution, an increase in n will increase the variance.

Stress Consider a binomial random variable X with n = 5 and p = 0.40, where X represents the number of times in the final exam week a student with 18 credit hours may feel stressed. -{Stress Narrative} Find the variance and standard deviation.

In Poisson experiment, the probability of more than one success in an interval approaches ____________________ as the interval becomes smaller.

The binomial random variable is the number of successes that occur in a fixed period of time.

Bivariate distributions provide probabilities of combinations of two variables.

Car Sales The joint probability distribution of variables X and Y is shown in the table below.Rebecca and Rachel are car salespeople.Let X denote the number of cars that Rebecca will sell in a month, and let Y denote the number of cars Rachel will sell in a month. 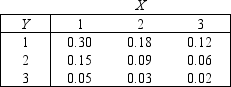-{Car Sales Narrative} Verify that V(X + Y) = V(X) + V(Y).Did you expect this result? Why?

In a Poisson experiment, the number of successes that occur in any interval of time is ____________________ of the number of success that occur in any other interval.

If n = 10 and p = 0.60, then the mean of the binomial distribution is

The expected number of heads in 100 tosses of an unbiased coin is

Golfing Store The joint probability distribution of variables X and Y is shown in the table below, where X is the number of drivers and Y is the number of putters sold daily in a small golfing store. 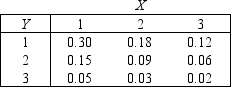-{Golfing Store Narrative} Calculate the variances of X and Y.

An auto insurance company evaluates many numerical variables about a person before deciding on an appropriate rate for automobile insurance.The number of claims a person has made in the last 3 years is an example of a(n) ____________________ random variable.

The largest value that a Poisson random variable X can have is n.

The number of days that a microcomputer goes without a breakdown is an example of a(n) ____________________ random variable.

911 Phone Calls 911 phone calls arrive at the rate of 30 per hour at the local call center. -{911 Phone Calls Narrative} Find the probability of receiving exactly eight calls in 15 minutes.