Exam 7: Random Variables and Discrete Probability Distributions

Car Sales The joint probability distribution of variables X and Y is shown in the table below.Rebecca and Rachel are car salespeople.Let X denote the number of cars that Rebecca will sell in a month, and let Y denote the number of cars Rachel will sell in a month. 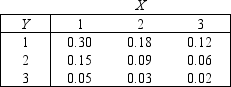-{Car Sales Narrative} Calculate E(X + Y) directly by using the probability distribution of X + Y.

Golfing Store The joint probability distribution of variables X and Y is shown in the table below, where X is the number of drivers and Y is the number of putters sold daily in a small golfing store. 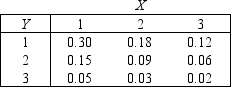-{Golfing Store Narrative} Find the probability distribution of the random variable X + Y.

Risky Undertaking Suppose you make a $2,000 investment in a risky undertaking.There is a 50% chance that the payoff from the investment will be $5,000, a 20% chance that you will just get your money back, and a 30% chance that you will receive nothing at all from your investment. -{Risky Undertaking Narrative} If you invest $6,000 in the risky undertaking instead of $2,000 and the possible payoffs triple accordingly, what are the expected value of the net profit from the $6,000 investment?

Number of Birds Alana and Eva are sisters.Let X denote the number of birds that Alana may have in the next two years, and let Y denote the number of birds Eva may have during the same period.The marginal probability distributions of X and Y are shown below. -{Number of Birds Narrative} Calculate E(XY) directly by using the probability distribution of XY.

Gym Visits Let X represent the number of times a student visits a gym in a one month period.Assume that the probability distribution of X is as follows: -{Gym Visits Narrative} What is the probability that the student visits the gym at least once in a month?

To find the probability that X is at most 10, you should find the probability that X is 10 or ____________________.

Elizabeth's Portfolio Elizabeth has decided to form a portfolio by putting 30% of her money into stock 1 and 70% into stock 2.She assumes that the expected returns will be 10% and 18%, respectively, and that the standard deviations will be 15% and 24%, respectively. -{Elizabeth's Portfolio Narrative} Compute the standard deviation of the returns on the portfolio assuming that the two stocks' returns are perfectly positively correlated.

Shopping Outlet A shopping outlet estimates the probability distribution of the number of stores shoppers actually enter as shown in the table below. -{Shopping Outlet Narrative} Use the laws of variance to calculate the variance and standard deviation of Y from the probability distribution of X.

Given that X is a discrete random variable, then the laws of expected value and variance can be applied to show that E(X + 5) = E(X) + 5, and V(X + 5) = V(X) + 25.

The covariance can be negative but the coefficient of correlation cannot.

Classified Department Phone Calls A classified department receives an average of 10 telephone calls each afternoon between 2 and 4 P.M.The calls occur randomly and independently of one another. -{Classified Department Phone Calls Narrative} Find the probability that the department will receive seven calls between 2 and 3 P.M.on a particular afternoon.

The variance of a binomial distribution for which n = 100 and p = 0.20 is:

The probability of a failure in a binomial experiment is denoted by ____________________.

The expected number of heads in 250 tosses of an unbiased coin is 125.

Shopping Outlet A shopping outlet estimates the probability distribution of the number of stores shoppers actually enter as shown in the table below. -{Shopping Outlet Narrative} Calculate the expected value of Y directly from the probability distribution of Y.

Shopping Outlet A shopping outlet estimates the probability distribution of the number of stores shoppers actually enter as shown in the table below. -{Shopping Outlet Narrative} Calculate the variance and standard deviation of Y directly from the probability distribution of Y.

Mobile Phones Sales After analyzing sales data, the owner of a Mobile Phone store produced the following joint probability distribution of the number of iPhones (X) and Blackberries (Y) sold daily. 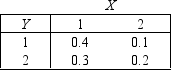-{Mobile Phones Sales Narrative} Compute the variance of the number of iPhones sold daily.

Shopping Outlet A shopping outlet estimates the probability distribution of the number of stores shoppers actually enter as shown in the table below. -{Shopping Outlet Narrative} Suppose Y = 2X + 1 for each value of X.What is the probability distribution of Y?

If X and Y are two variables with 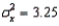, , 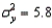and COV(X, Y) = 14.703, then the coefficient of correlation 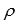= 0.78.

Number of Motorcycles The probability distribution of a discrete random variable X is shown below, where X represents the number of motorcycles owned by a family. -{Number of Motorcycles Narrative} Find the expected value of X.