Exam 11: Applications of Derivatives
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
A printer has a contract to print 62,000 posters for a political candidate. He can run the posters by using any number of plates from 1 to 30 on his press. If he uses x metal plates, they will produce x copies of the poster with each impression of the press. The metal plates cost $3.00 to prepare, and it costs $15.00 per hour to run the press. If the press can make 1000 impressions per hour, how many metal plates should the printer make to minimize costs? Round your answer to the nearest count of metal plates.
(Multiple Choice)
4.7/5  (42)
(42)
Assume that the total daily cost, in dollars, of producing plastic rafts for swimming pools is given by 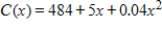 where x is the number of rafts produced per day, then the average cost per raft produced id given by
where x is the number of rafts produced per day, then the average cost per raft produced id given by 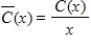 , for
, for 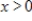 . Find the level of production that minimizes average cost.
. Find the level of production that minimizes average cost.
(Multiple Choice)
4.8/5  (36)
(36)
If the total revenue function for a blender is 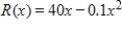 , find the maximum revenue if production is limited to at most 150 blenders.
, find the maximum revenue if production is limited to at most 150 blenders.
(Multiple Choice)
4.9/5  (28)
(28)
Use the graph of 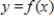 to identify at which of the indicated points the derivative
to identify at which of the indicated points the derivative 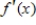 does not change sign.
does not change sign. 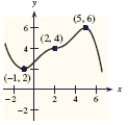
(Multiple Choice)
4.8/5  (36)
(36)
Both a function and its derivative are given. Use them to find all critical points. 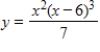
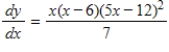
(Multiple Choice)
4.8/5  (42)
(42)
Analytically determine any relative minima. Round your answer to two decimal places. 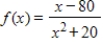
(Multiple Choice)
4.8/5  (26)
(26)
The running yard for a dog kennel must contain at least 900 square feet. If a 20-foot side of the kennel is used as part of one side of a rectangular yard with 900 square feet, what dimensions will require the least amount of fencing? Round your answer to the nearest feet.
(Multiple Choice)
4.9/5  (39)
(39)
Use the indicated x-values on the graph of 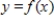 to find the x-coordinate of any horizontal point of inflection.
to find the x-coordinate of any horizontal point of inflection. 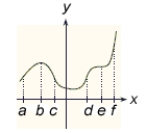
(Multiple Choice)
4.7/5  (36)
(36)
The percent p of impurities that can be removed from the waste water of a manufacturing process at a cost of C dollars is given by 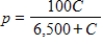 . Find any C values within the domain of the problem at which the rate of change of p with respect to C does not exist.
. Find any C values within the domain of the problem at which the rate of change of p with respect to C does not exist.
(Multiple Choice)
4.8/5  (34)
(34)
The number of milligrams x of a medication in the bloodstream t hours after a dose is taken can be modeled by 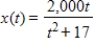 ,
, 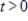 . For what
. For what  -values is
-values is  increasing? Round answers to two decimal places.
increasing? Round answers to two decimal places.
(Multiple Choice)
4.9/5  (47)
(47)
Use the graph of 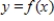 to identify at which of the indicated points the derivative
to identify at which of the indicated points the derivative 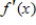 changes from positive to negative.
changes from positive to negative. 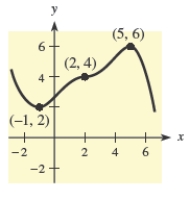
(Multiple Choice)
4.9/5  (35)
(35)
A function and its graph are given. Use the graph to find 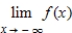 , if it exists, where
, if it exists, where 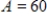 . Confirm your results analytically.
. Confirm your results analytically. 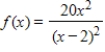
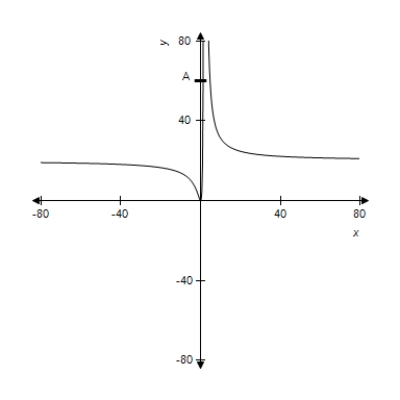
(Multiple Choice)
4.7/5  (35)
(35)
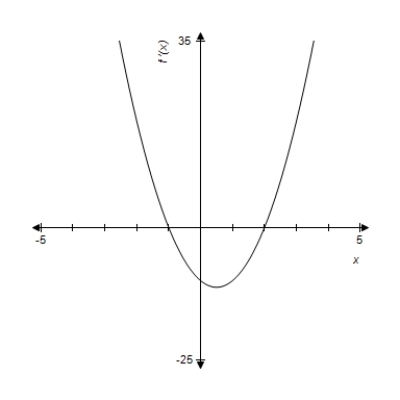
A graph of 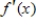 is given. Use the graph to determine all critical values of
is given. Use the graph to determine all critical values of 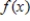 .
. 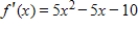
(Multiple Choice)
4.8/5  (45)
(45)
Both a function and its derivative are given. Use them to find intervals on which the function is increasing. 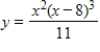
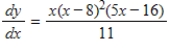
(Multiple Choice)
4.8/5  (44)
(44)
Use the graph shown in the figure and identify points from A through I that satisfy the given condition. 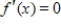 and
and 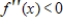
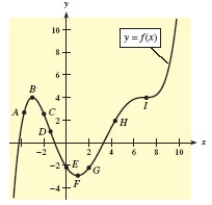
(Multiple Choice)
4.8/5  (36)
(36)
In this problem, 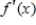 and its graph are given. Use the graph of
and its graph are given. Use the graph of 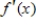 to determine where
to determine where 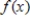 is concave down.
is concave down. 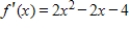
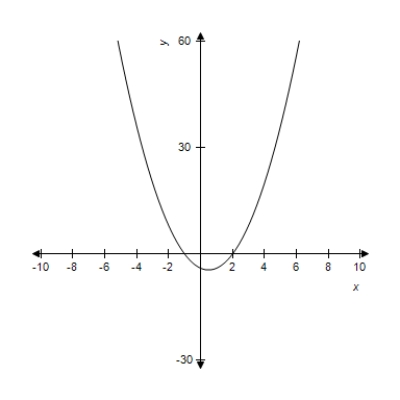
(Multiple Choice)
4.8/5  (35)
(35)
A function and its graph are given. Use the graph to find the horizontal asymptotes, if they exist. Confirm your results analytically. 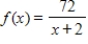
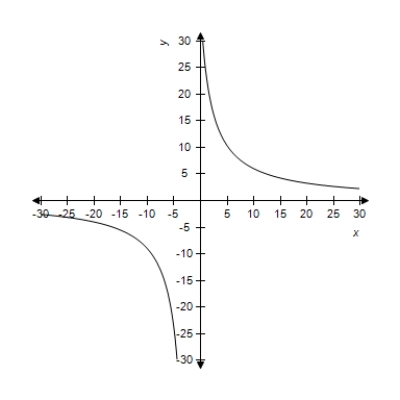
(Multiple Choice)
4.8/5  (48)
(48)
A rectangular area is to be enclosed and divided into thirds. The family has $800 to spend for the fencing material. The outside fence costs $18 per running foot installed, and the dividers cost $22 per running foot installed. What are the dimensions that will maximize the area enclosed? Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (44)
(44)
Showing 101 - 120 of 172
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)