Exam 11: Applications of Derivatives
Exam 1: Algebraic Concepts308 Questions
Exam 2: Linear Equations and Functions243 Questions
Exam 3: Quadratic and Other Special Functions113 Questions
Exam 4: Matrices227 Questions
Exam 5: Inequalities and Linear Programming120 Questions
Exam 6: Exponential and Logarithmic Functions108 Questions
Exam 7: Mathematics of Finance131 Questions
Exam 8: Introduction to Probability178 Questions
Exam 9: Further Topics in Probability; Data Description114 Questions
Exam 10: Derivatives248 Questions
Exam 11: Applications of Derivatives172 Questions
Exam 12: Derivatives Continued139 Questions
Exam 13: Indefinite Integrals120 Questions
Exam 14: Definite Integrals: Techniques of Integration185 Questions
Exam 15: Functions of Two or More Variables119 Questions
Select questions type
For the given function find the relative maxima, and sketch the graph. You may check your graph with a graphing utility. 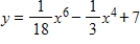
(Multiple Choice)
4.9/5  (33)
(33)
A function and its first and second derivatives are given. Use these to find any relative minima. 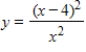
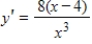
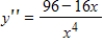
(Multiple Choice)
4.8/5  (39)
(39)
Make a sign diagram for the function and determine all x-values at which relative maxima occur. 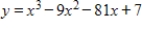
(Multiple Choice)
4.9/5  (34)
(34)
Suppose the average costs of a mining operation depend on the number of machines used, and average costs, in dollars, are given by 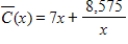 ,
, 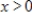 , where x is the number of machines used. What is the minimum average cost? Round your answer to the nearest dollar.
, where x is the number of machines used. What is the minimum average cost? Round your answer to the nearest dollar.
(Multiple Choice)
4.8/5  (32)
(32)
The following figure shows the growth of a population as a function of time. 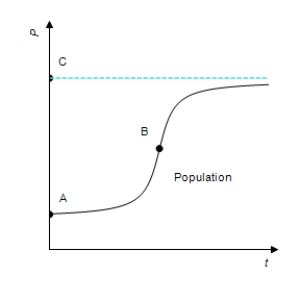 Which of A, B, and C correspond(s) to the point(s) at which the growth rate attains its maximum?
Which of A, B, and C correspond(s) to the point(s) at which the growth rate attains its maximum?
(Multiple Choice)
4.9/5  (45)
(45)
Suppose that a company needs 800 items during a year and that preparation for each production run costs $60. Suppose further that it costs $8 to produce each item and $0.45 to store an item for one year. Use the inventory cost model to find the number of items in each production run that will minimize the total costs of production and storage.
(Multiple Choice)
4.8/5  (34)
(34)
Suppose that the oxygen level P (for purity) in a body of water t months after an oil spill is given by 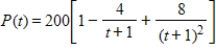 . Find how long it will be before the oxygen level reaches its minimum.
. Find how long it will be before the oxygen level reaches its minimum.
(Multiple Choice)
4.8/5  (37)
(37)
For the given function, use the graph to identify x-values for which 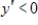 . You may use the derivative to check your conclusion.
. You may use the derivative to check your conclusion. 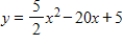
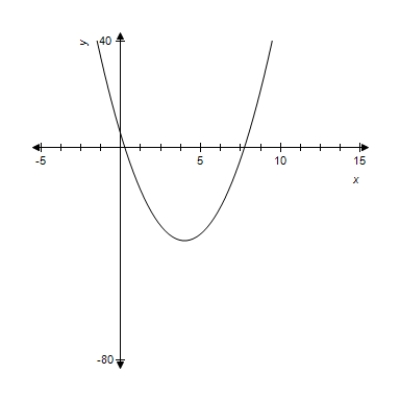
(Multiple Choice)
4.9/5  (31)
(31)
Analytically determine the location(s) of any horizontal asymptote(s). Round your answer to two decimal places. 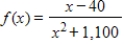
(Multiple Choice)
4.8/5  (33)
(33)
A time study showed that, on average, the productivity of a worker after t hours on the job can be modeled by 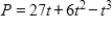 ,
, 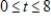 , where
, where 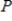 is the number of units produced per hour. After how many hours will productivity be maximized? Round your answer to two decimal places.
is the number of units produced per hour. After how many hours will productivity be maximized? Round your answer to two decimal places.
(Multiple Choice)
4.7/5  (43)
(43)
For the given function, classify the critical points as relative maxima, relative minima, or points of inflection. In each case, you may check your conclusions with a graphing utility. 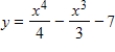
(Multiple Choice)
4.9/5  (36)
(36)
A firm has total revenue given by 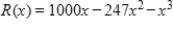 dollars for x units of a product. Find the maximum revenue from sales of that product.
dollars for x units of a product. Find the maximum revenue from sales of that product.
(Multiple Choice)
4.9/5  (41)
(41)
A product can be produced at a total cost 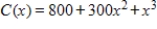 dollars, where x is the number produced. If the total revenue is given by
dollars, where x is the number produced. If the total revenue is given by 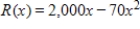 dollars, find the maximum profit. Round your answer to the nearest dollar.
dollars, find the maximum profit. Round your answer to the nearest dollar.
(Multiple Choice)
4.9/5  (43)
(43)
A small business has weekly average costs (in dollars) of 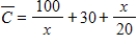 , where
, where  is the number of units produced each week. The competitive market price for this business's product is $41 per unit. If production is limited to 277 units per week, find the level of production that yields maximum profit.
is the number of units produced each week. The competitive market price for this business's product is $41 per unit. If production is limited to 277 units per week, find the level of production that yields maximum profit.
(Multiple Choice)
4.9/5  (38)
(38)
Both a function and its derivative are given. Use them to find all critical values. 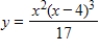
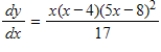
(Multiple Choice)
4.9/5  (47)
(47)
Showing 81 - 100 of 172
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)