Exam 20: Model Building
Exam 1: What Is Statistics14 Questions
Exam 2: Types of Data, Data Collection and Sampling16 Questions
Exam 3: Graphical Descriptive Methods Nominal Data19 Questions
Exam 4: Graphical Descriptive Techniques Numerical Data64 Questions
Exam 5: Numerical Descriptive Measures147 Questions
Exam 6: Probability106 Questions
Exam 7: Random Variables and Discrete Probability Distributions55 Questions
Exam 8: Continuous Probability Distributions117 Questions
Exam 9: Statistical Inference: Introduction8 Questions
Exam 10: Sampling Distributions65 Questions
Exam 11: Estimation: Describing a Single Population127 Questions
Exam 12: Estimation: Comparing Two Populations22 Questions
Exam 13: Hypothesis Testing: Describing a Single Population129 Questions
Exam 14: Hypothesis Testing: Comparing Two Populations78 Questions
Exam 15: Inference About Population Variances49 Questions
Exam 16: Analysis of Variance115 Questions
Exam 17: Additional Tests for Nominal Data: Chi-Squared Tests110 Questions
Exam 18: Simple Linear Regression and Correlation213 Questions
Exam 19: Multiple Regression121 Questions
Exam 20: Model Building92 Questions
Exam 21: Nonparametric Techniques126 Questions
Exam 22: Statistical Inference: Conclusion103 Questions
Exam 23: Time-Series Analysis and Forecasting145 Questions
Exam 24: Index Numbers25 Questions
Exam 25: Decision Analysis51 Questions
Select questions type
In the first-order model ŷ = 8 + 3x1 +5x2, a unit increase in , while holding constant, increases the value of on average by 3 units.
(True/False)
4.9/5  (42)
(42)
Consider the following data for two variables, x and y. x 7 10 3 5 3 10 4 14 5 8 y 35.0 28.5 45.0 45.0 55.0 25.0 37.5 27.5 30.0 27.5 Use Excel to develop an estimated regression equation of the form ? = b0 +b1x + b2x2..
(Essay)
4.8/5  (34)
(34)
A professor of accounting wanted to develop a multiple regression model to predict the students' grades in her fourth-year accounting course. She decides that the two most important factors are the student's grade point average (GPA) in the first three years and the student's major. She proposes the model: .
where
y
= fourth-year accounting course mark (out of 100). = GPA in first three years (range 0 to 12). = 1 if student's major is accounting.
= 0 if not. = 1 if student's major is finance.
= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS . Predictor Coef SDev T Constant 9.14 7.10 1.287 6.73 1.91 3.524 10.42 4.16 2.505 5.16 3.93 1.313 S = 15.0 R-Sq = 44.2%. ANALYSIS OF VARIANCE Source of Variation df SS MS F Regression 3 17098 5699.333 25.386 Error 96 21553 224.510 Total 99 38651 Do these results allow us to conclude at the 1% significance level that grade point average in the first three years is linearly related to fourth-year accounting course mark?
(Essay)
4.8/5  (41)
(41)
A professor of accounting wanted to develop a multiple regression model to predict the students' grades in her fourth-year accounting course. She decides that the two most important factors are the student's grade point average (GPA) in the first three years and the student's major. She proposes the model: .
where
y
= fourth-year accounting course mark (out of 100). = GPA in first three years (range 0 to 12). = 1 if student's major is accounting.
= 0 if not. = 1 if student's major is finance.
= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS . Predictor Coef SDev T Constant 9.14 7.10 1.287 6.73 1.91 3.524 10.42 4.16 2.505 5.16 3.93 1.313 S = 15.0 R-Sq = 44.2%. ANALYSIS OF VARIANCE Source of Variation df SS MS F Regression 3 17098 5699.333 25.386 Error 96 21553 224.510 Total 99 38651 Do these results allow us to conclude at the 1% significance level that on average accounting majors outperform those whose majors are not accounting or finance?
(Essay)
5.0/5  (36)
(36)
An economist is analysing the incomes of professionals (physicians, dentists and lawyers). He realises that an important factor is the number of years of experience. However, he wants to know if there are differences among the three professional groups. He takes a random sample of 125 professionals and estimates the multiple regression model: .
where
y
= annual income (in $1000). = years of experience. = 1 if physician.
= 0 if not. = 1 if dentist.
= 0 if not.
The computer output is shown below.
THE REGRESSION EQUATION IS . Predictor Coef SDev T Constant 71.65 18.56 3.860 2.07 0.81 2.556 10.16 3.16 3.215 -7.44 2.85 -2.611 S = 42.6 R-Sq = 30.9%. ANALYSIS OF VARIANCE Source of Variation df SS MS F Regression 3 98008 32669.333 18.008 Error 121 219508 1814.116 Total 124 317516 Is there enough evidence at the 5% significance level to conclude that income and experience are linearly related?
(Essay)
4.8/5  (35)
(35)
An indicator variable (also called a dummy variable) is a variable that can assume either one of two values (usually 0 and 1), where one value represents the existence of a certain condition, and the other value indicates that the condition does not hold.
(True/False)
4.8/5  (40)
(40)
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: .
Where:
y = number of annual fatalities per shire. = number of cars registered in the shire (in units of 10 000). = number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS . Predictor Coef SDev T Constant 69.7 41.3 1.688 11.3 5.1 2.216 7.61 2.55 2.984 -1.15 0.64 -1.797 -0.51 0.20 -2.55 -0.13 0.10 -1.30 S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE Source of df SS MS F Variation Regression 5 5959 1191.800 5.181 Error 29 6671 230.034 Total 34 12630 Test at the 1% significance level to determine whether the term should be retained in the model.
(Essay)
4.7/5  (33)
(33)
A traffic consultant has analysed the factors that affect the number of traffic fatalities. She has come to the conclusion that two important variables are the number of cars and the number of tractor-trailer trucks. She proposed the second-order model with interaction: .
Where:
y = number of annual fatalities per shire. = number of cars registered in the shire (in units of 10 000). = number of trucks registered in the shire (in units of 1000).
The computer output (based on a random sample of 35 shires) is shown below.
THE REGRESSION EQUATION IS . Predictor Coef SDev \multicolumn 1 c| T Constant 69.7 41.3 1.688 11.3 5.1 2.216 7.61 2.55 2.984 -1.15 0.64 -1.797 -0.51 0.20 -2.55 -0.13 0.10 -1.30 S = 15.2 R-Sq = 47.2%.
ANALYSIS OF VARIANCE Source of df SS MS F Variation Regression 5 5959 1191.800 5.181 Error 29 6671 230.034 Total 34 12630 What is the multiple coefficient of determination? What does this statistic tell you about the model?
(Essay)
4.9/5  (46)
(46)
In explaining the amount of money spent on children's toys during Christmas each year, the independent variable 'gender' is best represented by a dummy variable.
(True/False)
4.8/5  (40)
(40)
For the regression equation 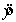 , which combination of and , respectively, results in the largest average value of y?
, which combination of and , respectively, results in the largest average value of y?
(Multiple Choice)
4.9/5  (39)
(39)
Which of the following is not an advantage of multiple regression as compared with analysis of variance?
(Multiple Choice)
4.7/5  (41)
(41)
The model 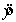 is referred to as a first-order model with two predictor variables with no interaction.
is referred to as a first-order model with two predictor variables with no interaction.
(True/False)
4.8/5  (35)
(35)
Consider the following data for two variables, x and y. x 7 10 3 5 3 10 4 14 5 8 y 35.0 28.5 45.0 45.0 55.0 25.0 37.5 27.5 30.0 27.5 Use Excel to determine whether there is sufficient evidence at the 1% significance level to infer that the relationship between y, x and in 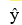 = 66.799 -7.307x + 0.324x2 is significant.
= 66.799 -7.307x + 0.324x2 is significant.
(Essay)
4.9/5  (38)
(38)
In the first-order model 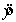 , a unit increase in , while holding constant at a value of 3, decreases the value of on average by 3 units.
, a unit increase in , while holding constant at a value of 3, decreases the value of on average by 3 units.
(True/False)
4.8/5  (32)
(32)
Consider the following data for two variables, x and y, where x is the age of a particular make of car
and y is the selling price, in thousands of dollars. x 7 10 3 5 3 10 4 14 5 8 y 35.0 28.5 45.0 45.0 55.0 25.0 37.5 27.5 30.0 27.5 a. Use Excel to develop an estimated regression equation of the form 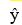 = b0 +b1x.
b. Interpret the intercept.
c. Interpret the slope.
= b0 +b1x.
b. Interpret the intercept.
c. Interpret the slope.
(Essay)
4.7/5  (40)
(40)
The following model + is used whenever the statistician believes that, on average, y is linearly related to:
(Multiple Choice)
4.7/5  (38)
(38)
An economist is in the process of developing a model to predict the price of gold. She believes that the two most important variables are the price of a barrel of oil and the interest rate She proposes the first-order model with interaction: . A random sample of 20 daily observations was taken. The computer output is shown below.
THE REGRESSION EQUATION IS
Predictor Coef S2Dev T Constant 115.6 78.1 1.480 22.3 7.1 3.141 14.7 6.3 2.333 -1.36 0.52 -2.615
ANALYSIS OF VARIANCE
Source of Variation df SS MS F Regression 3 8661 2887.0 6.626 Error 16 6971 435.7 Total 19 15632 Is there sufficient evidence at the 1% significance level to conclude that the interaction term should be retained?
(Essay)
4.7/5  (41)
(41)
Consider the following data for two variables, x and y. x 7 10 3 5 3 10 4 14 5 8 y 35.0 28.5 45.0 45.0 55.0 25.0 37.5 27.5 30.0 27.5 Use Excel to find the coefficient of determination. What does this statistic tell you about this curvilinear model?
(Essay)
4.8/5  (41)
(41)
The model 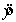 is referred to as a second-order model with two predictor variables with interaction.
is referred to as a second-order model with two predictor variables with interaction.
(True/False)
4.8/5  (30)
(30)
Showing 41 - 60 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)