Exam 19: Multiple Regression

A statistician wanted to determine whether the demographic variables of age, education and income influence the number of hours of television watched per week. A random sample of 25 adults was selected to estimate the multiple regression model $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$ . Where: y = number of hours of television watched last week. $x _ { 1 }$ = age. $x _ { 2 }$ = number of years of education. $X _ { 3 }$ = income (in $1000s). The computer output is shown below. THE REGRESSION EQUATION IS $y =$ $22.3 + 0.41 x _ { 1 } - 0.29 x _ { 2 } - 0.12 x _ { 3 }$ Predictor Coef StDev Constant 22.3 10.7 2.084 0.41 0.19 2.158 -0.29 0.13 -2.231 -0.12 0.03 -4.00 S = 4.51 R-Sq = 34.8%. ANALYSIS OF VARIANCE Source of Variation df SS MS F Regression 3 227 75.667 3.730 Error 21 426 20.286 Total 24 653 What is the coefficient of determination? What does this statistic tell you?

In a multiple regression problem involving 24 observations and three independent variables, the estimated regression equation is 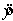$= 72 + 3.2 x _ { 1 } + 1.5 x _ { 2 } - x _ { 3 }$ . For this model, SST = 800 and SSE = 245. The value of the F-statistic for testing the significance of this model is 15.102.

Test the hypotheses: $H _ { 0 } :$ There is no first-order autocorrelation $H _ { 1 } :$ There is positive first-order autocorrelation, given that: the Durbin-Watson statistic d = 0.686, n = 16, k = 1 and $\alpha =$ 0.05.

Which of the following is not true when we add an independent variable to a multiple regression model?

In a multiple regression analysis, there are 20 data points and 4 independent variables, and the sum of the squared differences between observed and predicted values of y is 180. The multiple standard error of estimate will be:

Excel and Minitab both provide the p-value for testing each coefficient in the multiple regression model. In the case of $b _ { 2 }$ , this represents the probability that:

Which of the following best describes the ratio MSR/MSE in a multiple linear regression model?

A multiple regression the coefficient of determination is 0.81. The percentage of the variation in $y$ that is explained by the regression equation is 81%.

For a multiple regression model, the following statistics are given: Total variation in y = SSY = 250, SSE = 50, k = 4, n = 20. The coefficient of determination adjusted for degrees of freedom is:

In a multiple regression analysis, if the model provides a poor fit, this indicates that:

In multiple regression, the descriptor 'multiple' refers to more than one independent variable.

Which of the following best explains a small F-statistic when testing the validity of a multiple regression model?

The most commonly used method to remedy non-normality or heteroscedasticity in regression analysis is to transform the dependent variable. The most commonly used transformations are $y ^ { \prime } = \log y ( \text { provided } y \geq 0 )$ , $y ^ { \prime } = y ^ { 2 }$ , $y ^ { \prime } = \sqrt { y } ( \text { provided } y \geq 0 )$ , and $y ^ { \prime } = 1 / y$ .

A statistician wanted to determine whether the demographic variables of age, education and income influence the number of hours of television watched per week. A random sample of 25 adults was selected to estimate the multiple regression model $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$ . Where: y = number of hours of television watched last week. $x _ { 1 }$ = age. $x _ { 2 }$ = number of years of education. $X _ { 3 }$ = income (in $1000s). The computer output is shown below. THE REGRESSION EQUATION IS $y =$ $22.3 + 0.41 x _ { 1 } - 0.29 x _ { 2 } - 0.12 x _ { 3 }$ Predictor Coef StDev Constant 22.3 10.7 2.084 0.41 0.19 2.158 -0.29 0.13 -2.231 -0.12 0.03 -4.00 S = 4.51 R-Sq = 34.8%. ANALYSIS OF VARIANCE Source of Variation df SS MS F Regression 3 227 75.667 3.730 Error 21 426 20.286 Total 24 653 Test the overall validity of the model at the 5% significance level.

A statistics professor investigated some of the factors that affect an individual student's final grade in his or her course. He proposed the multiple regression model: $y = \beta _ { 0 } + \beta _ { 1 } x _ { 1 } + \beta _ { 2 } x _ { 2 } + \beta _ { 3 } x _ { 3 } + \varepsilon$ . Where: y = final mark (out of 100). $x _ { 1 }$ = number of lectures skipped. $x _ { 2 }$ = number of late assignments. $X _ { 3 }$ = mid-term test mark (out of 100). The professor recorded the data for 50 randomly selected students. The computer output is shown below. THE REGRESSION EQUATION IS 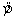= $41.6 - 3.18 x _ { 1 } - 1.17 x _ { 2 } + .63 x _ { 3 }$ Predictor Coef StDev T Constant 41.6 17.8 2.337 -3.18 1.66 -1.916 -1.17 1.13 -1.035 0.63 0.13 4.846 S = 13.74 R-Sq = 30.0%. ANALYSIS OF VARIANCE Source of Variation df SS MS F Regression 3 3716 1238.667 6.558 Error 46 8688 188.870 Total 49 12404 Do these data provide enough evidence at the 5% significance level to conclude that the final mark and the number of late assignments are negatively linearly related?

In a multiple regression analysis involving 25 data points and 5 independent variables, the sum of squares terms are calculated as: total variation in y = SSY = 500, SSR = 300, and SSE = 200. In testing the validity of the regression model, the F-value of the test statistic will be:

Which of the following best describes first-order autocorrelation?

In multiple regression models, the values of the error variable $\varepsilon$ are assumed to be:

Given the following statistics of a multiple regression model, can we conclude at the 5% significance level that $x _ { 1 }$ and y are linearly related? n = 42 k = 6 $b _ { 1 } =$ -5.30 $s _ { b _ { 1 } } =$ 1.5

In a multiple regression analysis involving 40 observations and 5 independent variables, total variation in y = SSY = 350 and SSE = 50. The multiple coefficient of determination is: