Exam 18: Simple Linear Regression and Correlation
Exam 1: What Is Statistics16 Questions
Exam 2: Types of Data, Data Collection and Sampling17 Questions
Exam 3: Graphical Descriptive Methods Nominal Data20 Questions
Exam 4: Graphical Descriptive Techniques Numerical Data64 Questions
Exam 5: Numerical Descriptive Measures150 Questions
Exam 6: Probability112 Questions
Exam 7: Random Variables and Discrete Probability Distributions55 Questions
Exam 8: Continuous Probability Distributions118 Questions
Exam 9: Statistical Inference: Introduction8 Questions
Exam 10: Sampling Distributions68 Questions
Exam 11: Estimation: Describing a Single Population132 Questions
Exam 12: Estimation: Comparing Two Populations23 Questions
Exam 13: Hypothesis Testing: Describing a Single Population130 Questions
Exam 14: Hypothesis Testing: Comparing Two Populations81 Questions
Exam 15: Inference About Population Variances47 Questions
Exam 16: Analysis of Variance125 Questions
Exam 17: Additional Tests for Nominal Data: Chi-Squared Tests116 Questions
Exam 18: Simple Linear Regression and Correlation219 Questions
Exam 19: Multiple Regression121 Questions
Exam 20: Model Building100 Questions
Exam 21: Nonparametric Techniques136 Questions
Exam 22: Statistical Inference: Conclusion106 Questions
Exam 23: Time-Series Analysis and Forecasting146 Questions
Exam 24: Index Numbers27 Questions
Exam 25: Decision Analysis51 Questions
Select questions type
Given the following linear regression model of Weekly sales ($000's) in a fast food restaurant against number of vouchers printed in the local newspaper, interpret the intercept. Does this make sense?
Estimated Sales = 11.5676 + 0.4618.Vouchers
(Essay)
4.8/5  (36)
(36)
If the value of the sum of squares for error, SSE, equals zero, then the coefficient of determination must equal zero.
(True/False)
4.8/5  (30)
(30)
In simple linear regression, which of the following statements indicates no linear relationship between the variables x and y? A. The coefficient of determination is 1.0 . B. The coefficient of correlation is 0.0 . C. The sum of squares for error is 0.0 . D. The sum of squares for regression is relatively large.
(Short Answer)
4.8/5  (36)
(36)
On the least squares regression line Estimated y= 2 - 3x, the predicted value of y equals: A. -1.0\nobreakspacewhen\nobreakspacex=-1.0.\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace\nobreakspace B. 1.0\nobreakspacewhen\nobreakspacex=1.0. C. 5.0\nobreakspacewhen\nobreakspacex=-1.0. D. 5.0\nobreakspacewhen\nobreakspacex=1.0.
(Short Answer)
4.8/5  (23)
(23)
Correlation analysis is used to determine the strength of a non-linear relationship between an independent variable x and a dependent variable y.
(True/False)
4.8/5  (34)
(34)
A professor of economics wants to study the relationship between income y (in $1000s) and education x (in years). A random sample of eight individuals is taken and the results are shown below. Education 16 11 15 8 12 10 13 14 Income 58 40 55 35 43 41 52 49 Determine the coefficient of determination, and discuss what its value tells you about the two variables.
(Essay)
4.7/5  (46)
(46)
A medical statistician wanted to examine the relationship between the amount of sunshine (x) and incidence of skin cancer (y). As an experiment he found the number of skin cancers detected per 100 000 of population and the average daily sunshine in eight country towns around NSW. These data are shown below. Average daily sunshine (hours) 5 7 6 7 8 6 4 3 Skin cancer per 100000 7 11 9 12 15 10 7 5 Calculate the coefficient of determination and interpret it.
(Essay)
4.8/5  (35)
(35)
In order to estimate with 95% confidence a particular value of for a given value of in a simple linear regression problem, a random sample of 20 observations is taken. The appropriate table value that would be used is 2.101.
(True/False)
4.7/5  (29)
(29)
Given that SSE = 84 and SSR = 358.12, the coefficient of correlation (also called the Pearson coefficient of correlation) must be 0.90.
(True/False)
4.8/5  (33)
(33)
A statistician investigating the relationship between the amount of precipitation (in inches) and the number of car accidents gathered data for 10 randomly selected days. The results are presented below. Day Precipitation Number of accidents 1 0.05 5 2 0.12 6 3 0.05 2 4 0.08 4 5 0.10 8 6 0.35 14 7 0.15 7 8 0.30 13 9 0.10 7 10 0.20 10 Calculate the standard error of estimate, and describe what this statistic tells you about the regression line.
(Essay)
4.9/5  (26)
(26)
The manager of a fast food restaurant wants to determine how sales in a given week are related to the number of discount vouchers (#) printed in the local newspaper during the week. The number of vouchers and sales ($000s) from 10 randomly selected weeks is given below with Excel regression output. Number of vouchers Sales 4 12.8 7 15.4 5 13.9 3 11.2 19 18.7 10 17.9 8 16.8 6 15.9 3 11.5 5 13.9 SUMMARY OUTPUT Regression Statistics Multiple R 0.8524 R Square 0.7267 Adjuted R Square 0.6925 Standard Error 1.4301 Observations 10.0000 ANOVA Sgnificance df SS MS F F Regression 1.0000 43.4982 43.4982 21.2682 0.0017 Residual 8.0000 16.3618 2.0452 Total 9.0000 59.8600 Coefficients Standard Error t Stat P-value Lower 95\% Upper 95\% Interoept 11.5676 0.8341 13.8679 0.0000 9.6441 13.4912 Number of voudhers 0.4618 0.1001 4.6117 0.0017 0.2309 0.6927 Interpret the coefficient of determination.
(Essay)
4.9/5  (36)
(36)
The vertical spread of the data points about the regression line is measured by the y-intercept.
(True/False)
4.8/5  (36)
(36)
The Spearman rank correlation coefficient must be used to determine whether a relationship exists between two variables when: A. one of the variables may be ordinal. B. both of the variables may be ordinal. C. both variables are interval and the normality requirement may not be satisfied. D. All of these choices are correct.
(Short Answer)
4.9/5  (41)
(41)
If the coefficient of correlation is −0.50, the percentage of the variation in the dependent variable y that is explained by the variation in the independent variable x is: A. -50\% B. 25\%. C. 50\% D. -25\%.
(Short Answer)
4.9/5  (36)
(36)
A medical statistician wanted to examine the relationship between the amount of sunshine (x) and incidence of skin cancer (y). As an experiment he found the number of skin cancers detected per 100 000 of population and the average daily sunshine in eight country towns around NSW. These data are shown below. Average daily sunshine (hours) 5 7 6 7 8 6 4 3 Skin cancer per 100000 7 11 9 12 15 10 7 5 Calculate the standard error of estimate, and describe what this statistic tells you about the regression line.
(Essay)
4.7/5  (39)
(39)
When the actual values y of a dependent variable and the corresponding predicted values 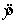 are the same, the standard error of the estimate will be 1.0.
are the same, the standard error of the estimate will be 1.0.
(True/False)
4.8/5  (46)
(46)
Which value of the coefficient of correlation r indicates a stronger correlation than − 0.85? A. -0.50 B. 0.75 C. -0.90 D. 0.85
(Short Answer)
4.8/5  (25)
(25)
A professor of economics wants to study the relationship between income y (in $1000s) and education x (in years). A random sample of eight individuals is taken and the results are shown below. Education 16 11 15 8 12 10 13 14 Income 58 40 55 35 43 41 52 49 Use the predicted and actual values of y to calculate the residuals.
(Essay)
4.8/5  (35)
(35)
The confidence interval estimate of the expected value of y will be narrower than the prediction interval for the same given value of x and confidence level. This is because there is less error in estimating a mean value than in predicting an individual value.
(True/False)
4.9/5  (35)
(35)
In order to estimate with 95% confidence the expected value of y in a simple linear regression problem, a random sample of 10 observations is taken. Which of the following t-table values listed below would be used? A. 2.228. B. 2.306. C. 1.860. D. 1.812.
(Short Answer)
4.9/5  (43)
(43)
Showing 101 - 120 of 219
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)