Exam 18: Simple Linear Regression and Correlation
Exam 1: What Is Statistics16 Questions
Exam 2: Types of Data, Data Collection and Sampling17 Questions
Exam 3: Graphical Descriptive Methods Nominal Data20 Questions
Exam 4: Graphical Descriptive Techniques Numerical Data64 Questions
Exam 5: Numerical Descriptive Measures150 Questions
Exam 6: Probability112 Questions
Exam 7: Random Variables and Discrete Probability Distributions55 Questions
Exam 8: Continuous Probability Distributions118 Questions
Exam 9: Statistical Inference: Introduction8 Questions
Exam 10: Sampling Distributions68 Questions
Exam 11: Estimation: Describing a Single Population132 Questions
Exam 12: Estimation: Comparing Two Populations23 Questions
Exam 13: Hypothesis Testing: Describing a Single Population130 Questions
Exam 14: Hypothesis Testing: Comparing Two Populations81 Questions
Exam 15: Inference About Population Variances47 Questions
Exam 16: Analysis of Variance125 Questions
Exam 17: Additional Tests for Nominal Data: Chi-Squared Tests116 Questions
Exam 18: Simple Linear Regression and Correlation219 Questions
Exam 19: Multiple Regression121 Questions
Exam 20: Model Building100 Questions
Exam 21: Nonparametric Techniques136 Questions
Exam 22: Statistical Inference: Conclusion106 Questions
Exam 23: Time-Series Analysis and Forecasting146 Questions
Exam 24: Index Numbers27 Questions
Exam 25: Decision Analysis51 Questions
Select questions type
A consultant for a beer company wanted to determine whether those who drink a lot of beer actually enjoy the taste more than those who drink moderately or rarely. She took a random sample of eight men and asked each how many beers they typically drink per week. She also asked them to rate their favourite brand of beer on a 10-point scale (1 = bad, 10 = excellent). The results are shown below. Can we infer at the 5% significance level that frequent beer drinkers rate their favourite beer more highly than less frequent drinkers? Beer drinker Typical weekly consumption Rating 1 4 6 2 3 6 3 12 9 4 15 8 5 7 8 6 9 6 7 1 5 8 10 8
(Essay)
4.9/5  (30)
(30)
We standardise residuals in the same way that we standardise all variables, by subtracting the mean and dividing by the variance.
(True/False)
4.9/5  (30)
(30)
An ardent fan of television game shows has observed that, in general, the more educated the contestant, the less money he or she wins. To test her belief, she gathers data about the last eight winners of her favourite game show. She records their winnings in dollars and their years of education. The results are as follows. Contestant Years of education Winnings 1 11 750 2 15 400 3 12 600 4 16 350 5 11 800 6 16 300 7 13 650 8 14 400 Calculate the Pearson correlation coefficient. What sign does it have? Why?
(Essay)
4.7/5  (29)
(29)
A financier whose specialty is investing in movie productions has observed that, in general, movies with 'big-name' stars seem to generate more revenue than those movies whose stars are less well known. To examine his belief, he records the gross revenue and the payment (in $ million) given to the two highest-paid performers in the movie for 10 recently released movies. Movie Cost of two highest- paid performers (\ ) Gross revenue (\ ) 1 5.3 48 2 7.2 65 3 1.3 18 4 1.8 20 5 3.5 31 6 2.6 26 7 8.0 73 8 2.4 23 9 4.5 39 10 6.7 58 Use the regression equation to determine the predicted values of y.
(Essay)
4.8/5  (33)
(33)
If the coefficient of determination is 81%, and the linear regression model has a negative slope, what is the value of the coefficient of correlation? A -0.81 B 0.90 C 0.81 D -0.90
(Short Answer)
4.9/5  (39)
(39)
If all the values of an independent variable x are equal, then regressing a dependent variable y on x will result in a coefficient of determination of 100%.
(True/False)
4.8/5  (30)
(30)
A regression analysis between height y (in cm) and age x (in years) of 2 to 10 years old boys yielded the least squares line y-hat = 87 + 6.5x. This implies that by each additional year height is expected to: \begin{array}{|l|l|}\hline A&\text {increase by 93.5 \mathrm{~cm} . }\\\hline B&\text {increase by \( 6.5 \mathrm{~cm} \). }\\\hline C&\text {increase by \( 87 \mathrm{~cm} \). }\\\hline D&\text {decrease by \( 6.5 \mathrm{~cm} \). }\\\hline \end{array}
(Short Answer)
4.8/5  (38)
(38)
A direct relationship between an independent variable x and a dependent variably y means that x and y move in the same directions.
(True/False)
4.8/5  (27)
(27)
A statistician investigating the relationship between the amount of precipitation (in inches) and the number of car accidents gathered data for 10 randomly selected days. The results are presented below. Day Precipitation Number of accidents 1 0.05 5 2 0.12 6 3 0.05 2 4 0.08 4 5 0.10 8 6 0.35 14 7 0.15 7 8 0.30 13 9 0.10 7 10 0.20 10 Do these data allow us to conclude at the 10% significance level that the amount of precipitation and the number of accidents are linearly related?
(Essay)
4.7/5  (33)
(33)
A financier whose specialty is investing in movie productions has observed that, in general, movies with 'big-name' stars seem to generate more revenue than those movies whose stars are less well known. To examine his belief, he records the gross revenue and the payment (in $ million) given to the two highest-paid performers in the movie for 10 recently released movies. Movie Cost of two highest- paid performers (\ ) Gross revenue (\ ) 1 5.3 48 2 7.2 65 3 1.3 18 4 1.8 20 5 3.5 31 6 2.6 26 7 8.0 73 8 2.4 23 9 4.5 39 10 6.7 58 Calculate the Pearson correlation coefficient. What sign does it have? Why?
(Essay)
4.9/5  (37)
(37)
A professor of economics wants to study the relationship between income y (in $1000s) and education x (in years). A random sample of eight individuals is taken and the results are shown below. Education 16 11 15 8 12 10 13 14 Income 58 40 55 35 43 41 52 49 Draw a scatter diagram of the data to determine whether a linear model appears to be appropriate.
(Essay)
4.9/5  (34)
(34)
Another name for the residual term in a regression equation is random error.
(True/False)
4.8/5  (40)
(40)
If the sum of squared residuals is zero, then the: A. coefficient of determination must be 1.0 . B. coefficient of correlation must be 1.0 . C. coefficient of determination must be 0.0 . D. coefficient of correlation must be 0.0 .
(Short Answer)
4.7/5  (25)
(25)
In a regression problem the following pairs (x,y) are given: (1,2), (2.5,2), (3,2), (5,2) and (5.3,2). This indicates that the: A. correlation coefficient is 0 . B. correlation coefficient is 1 . C. correlation coefficient is -1 . D. coefficient of determination is between 0 and 1 .
(Short Answer)
5.0/5  (39)
(39)
A professor of economics wants to study the relationship between income y (in $1000s) and education x (in years). A random sample of eight individuals is taken and the results are shown below. Education 16 11 15 8 12 10 13 14 Income 58 40 55 35 43 41 52 49 Conduct a test of the population coefficient of correlation to determine at the 5% significance level whether a linear relationship exists between years of education and income.
(Essay)
4.8/5  (38)
(38)
A regression analysis between sales (in $1000) and advertising (in $) yielded the least squares line 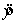 in sales. }\\ \hline B&\text { increase in advertising is expected to result in an increase of in sales.}\\ \hline C&\text { increase of in advertising is expected to result in an increase of in sales. }\\ \hline D&\text {increase of in advertising is expected to result in an increase of in sales. }\\ \hline \end{array} " class="answers-bank-image d-inline" loading="lazy" > = 80 000 + 5x. This implies that an: A increase of \ 1 in advertising is expected to result in an increase of \ 5 in sales. B increase \ 5 in advertising is expected to result in an increase of \ 5000 in sales. C increase of \ 1 in advertising is expected to result in an increase of \ 80005 in sales. D increase of \ 1 in advertising is expected to result in an increase of \ 5000 in sales.
in sales. }\\ \hline B&\text { increase in advertising is expected to result in an increase of in sales.}\\ \hline C&\text { increase of in advertising is expected to result in an increase of in sales. }\\ \hline D&\text {increase of in advertising is expected to result in an increase of in sales. }\\ \hline \end{array} " class="answers-bank-image d-inline" loading="lazy" > = 80 000 + 5x. This implies that an: A increase of \ 1 in advertising is expected to result in an increase of \ 5 in sales. B increase \ 5 in advertising is expected to result in an increase of \ 5000 in sales. C increase of \ 1 in advertising is expected to result in an increase of \ 80005 in sales. D increase of \ 1 in advertising is expected to result in an increase of \ 5000 in sales.
(Short Answer)
4.7/5  (41)
(41)
The variance of the error variable, , is required to be constant. When this requirement is satisfied, the condition is called homoscedasticity.
(True/False)
4.8/5  (32)
(32)
A professor of economics wants to study the relationship between income y (in $1000s) and education x (in years). A random sample of eight individuals is taken and the results are shown below. Education 16 11 15 8 12 10 13 14 Income 58 40 55 35 43 41 52 49 Calculate the Pearson correlation coefficient. What sign does it have? Why?
(Essay)
4.8/5  (38)
(38)
In regression analysis, if the coefficient of determination is 1.0, then: A. the sum of squares for error must be 1.0 . B. the sum of squares for regression must be 1.0. C. the sum of squares for error must be 0.0 . D. the sum of squares for regression must be 0.0 .
(Short Answer)
4.8/5  (26)
(26)
An outlier is an observation that is unusually small or unusually large.
(True/False)
4.8/5  (43)
(43)
Showing 41 - 60 of 219
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)