Exam 6: Distribution and Network Models
Exam 1: Introduction63 Questions
Exam 2: An Introduction to Linear Programming66 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution56 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management63 Questions
Exam 5: Advanced Linear Programming Applications46 Questions
Exam 6: Distribution and Network Models70 Questions
Exam 7: Integer Linear Programming61 Questions
Exam 8: Nonlinear Optimization Models51 Questions
Exam 9: Project Scheduling: Pertcpm59 Questions
Exam 10: Inventory Models65 Questions
Exam 11: Waiting Line Models68 Questions
Exam 12: Simulation62 Questions
Exam 13: Decision Analysis97 Questions
Exam 14: Multicriteria Decisions50 Questions
Exam 15: Time Series Analysis and Forecasting63 Questions
Exam 16: Markov Processes49 Questions
Exam 17: Linear Programming: Simplex Method51 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality35 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems44 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming38 Questions
Select questions type
The problem which deals with the distribution of goods from several sources to several destinations is the
(Multiple Choice)
4.7/5  (30)
(30)
Fodak must schedule its production of camera film for the first four months of the year. Film demand (in 1,000s of rolls) in January, February, March and April is expected to be 300, 500, 650 and 400, respectively. Fodak's production capacity is 500 thousand rolls of film per month. The film business is highly competitive, so Fodak cannot afford to lose sales or keep its customers waiting. Meeting month i 's demand with month i +1's production is unacceptable.
Film produced in month i can be used to meet demand in month i or can be held in inventory to meet demand in month i +1 or month i +2 (but not later due to the film's limited shelflife). There is no film in inventory at the start of January.
The film's production and delivery cost per thousand rolls will be $500 in January and February. This cost will increase to $600 in March and April due to a new labor contract. Any film put in inventory requires additional transport costing $100 per thousand rolls. It costs $50 per thousand rolls to hold film in inventory from one month to the next.
a.
Modeling this problem as a transshipment problem, draw the network representation.
b.
Formulate and solve this problem as a linear program.
(Essay)
4.7/5  (37)
(37)
A foreman is trying to assign crews to produce the maximum number of parts per hour of a certain product. He has three crews and four possible work centers. The estimated number of parts per hour for each crew at each work center is summarized below. Solve for the optimal assignment of crews to work centers. 
(Essay)
4.9/5  (26)
(26)
Draw the network for this assignment problem.
Min
10x1A + 12x1B + 15x1C + 25x1D + 11x2A + 14x2B + 19x2C + 32x2D
+ 18x3A + 21x3B + 23x3C + 29x3D + 15x4A + 20x4B + 26x4C + 28x4D
s.t.
x1A + x1B + x1C + x1D = 1
x2A + x2B + x2C + x2D = 1
x3A + x3B + x3C + x3D = 1
x4A + x4B + x4C + x4D = 1
x1A + x2A + x3A + x4A = 1
x1B + x 2B + x3B + x4B = 1
x1C + x 2C + x3C + x4C = 1
x1D + x2D + x3D + x4D = 1
(Essay)
4.8/5  (30)
(30)
A dummy origin in a transportation problem is used when supply exceeds demand.
(True/False)
4.9/5  (29)
(29)
Consider a maximal flow problem in which vehicle traffic entering a city is routed among several routes before eventually leaving the city. When represented with a network,
(Multiple Choice)
4.9/5  (27)
(27)
A clothing distributor has four warehouses which serve four large cities. Each warehouse has a monthly capacity of 5,000 blue jeans. They are considering using a transportation LP approach to match demand and capacity. The following table provides data on their shipping cost, capacity, and demand constraints on a per-month basis. Develop a linear programming model for this problem.
? 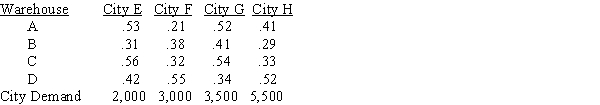
(Essay)
4.8/5  (41)
(41)
Is it a coincidence to obtain integer solutions to network problems? Explain.
(Short Answer)
4.9/5  (40)
(40)
Canning Transport is to move goods from three factories to three distribution centers. Information about the move is given below. Give the network model and the linear programming model for this problem. 
Shipping costs are:
Shipping costs are: 
(Essay)
4.9/5  (35)
(35)
A transportation problem with 3 sources and 4 destinations will have 7 decision variables.
(True/False)
4.8/5  (30)
(30)
Draw the network for this transportation problem.
Min
2XAX + 3XAY + 5XAZ+ 9XBX + 12XBY + 10XBZ
s.t.
XAX + XAY + XAZ ≤ 500
X BX + XBY + XBZ ≤ 400
XAX + XBX = 300
XAY + XBY = 300
XAZ + XBZ = 300
Xij ≥ 0
(Essay)
4.7/5  (31)
(31)
Consider the network below. Formulate the LP for finding the shortest-route path from node 1 to node 7.
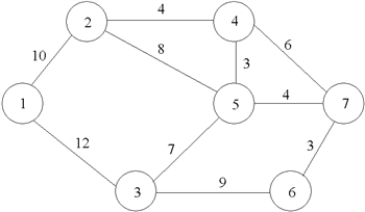
(Essay)
4.9/5  (33)
(33)
In the general linear programming model of the assignment problem,
(Multiple Choice)
4.8/5  (39)
(39)
The maximal flow problem can be formulated as a capacitated transshipment problem.
(True/False)
4.9/5  (28)
(28)
In the general assignment problem, one agent can be assigned to several tasks.
(True/False)
4.9/5  (27)
(27)
In a transportation problem with total supply equal to total demand, if there are four origins and seven destinations, and there is a unique optimal solution, the optimal solution will utilize 11 shipping routes.
(True/False)
4.9/5  (36)
(36)
Showing 41 - 60 of 70
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)