Exam 6: Distribution and Network Models
Exam 1: Introduction63 Questions
Exam 2: An Introduction to Linear Programming66 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution56 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management63 Questions
Exam 5: Advanced Linear Programming Applications46 Questions
Exam 6: Distribution and Network Models70 Questions
Exam 7: Integer Linear Programming61 Questions
Exam 8: Nonlinear Optimization Models51 Questions
Exam 9: Project Scheduling: Pertcpm59 Questions
Exam 10: Inventory Models65 Questions
Exam 11: Waiting Line Models68 Questions
Exam 12: Simulation62 Questions
Exam 13: Decision Analysis97 Questions
Exam 14: Multicriteria Decisions50 Questions
Exam 15: Time Series Analysis and Forecasting63 Questions
Exam 16: Markov Processes49 Questions
Exam 17: Linear Programming: Simplex Method51 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality35 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems44 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming38 Questions
Select questions type
Which of the following is not true regarding the linear programming formulation of a transportation problem?
(Multiple Choice)
4.9/5  (32)
(32)
In a capacitated transshipment problem, some or all of the transfer points are subject to capacity restrictions.
(True/False)
4.8/5  (35)
(35)
Peaches are to be transported from three orchard regions to two canneries. Intermediate stops at a consolidation station are possible. 
Shipment costs are shown in the table below. Where no cost is given, shipments are not possible. Where costs are shown, shipments are possible in either direction. Draw the network model for this problem.
Shipment costs are shown in the table below. Where no cost is given, shipments are not possible. Where costs are shown, shipments are possible in either direction. Draw the network model for this problem. 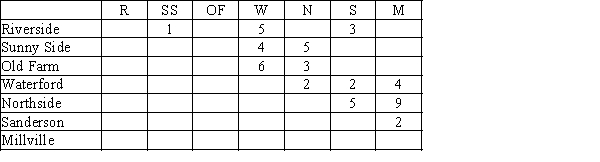
(Essay)
4.7/5  (38)
(38)
A transportation problem with 3 sources and 4 destinations will have 7 variables in the objective function.
(True/False)
4.9/5  (28)
(28)
Explain how the general linear programming model of the assignment problem can be modified to handle problems
involving a maximization function, unacceptable assignments, and supply not equally demand.
(Essay)
4.9/5  (31)
(31)
A network of railway lines connects the main lines entering and leaving a city. Speed limits, track reconstruction, and train length restrictions lead to the flow diagram below, where the numbers represent how many cars can pass per hour. Formulate an LP to find the maximal flow in cars per hour from Node 1 to Node F.
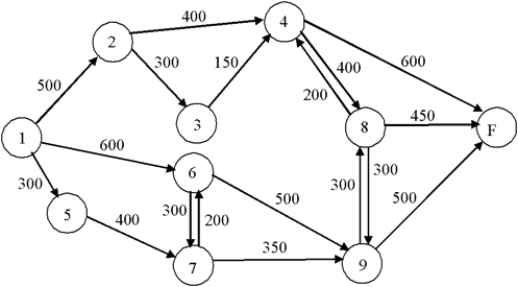
(Essay)
4.8/5  (30)
(30)
The network flows into and out of demand nodes are what makes the production and inventory application modeled in the textbook a
(Multiple Choice)
4.8/5  (33)
(33)
Consider a shortest route problem in which a bank courier must travel between branches and the main operations center. When represented with a network,
(Multiple Choice)
5.0/5  (33)
(33)
If a transportation problem has four origins and five destinations, the LP formulation of the problem will have
(Multiple Choice)
4.8/5  (37)
(37)
Consider the following shortest-route problem involving six cities with the distances given. Draw the network for this problem and formulate the LP for finding the shortest distance from City 1 to City 6. 
(Essay)
4.9/5  (38)
(38)
A plant manager for a sporting goods manufacturer is in charge of assigning the manufacture of four new aluminum products to four different departments. Because of varying expertise and workloads, the different departments can produce the new products at various rates. If only one product is to be produced by each department and the daily output rates are given in the table below, which department should manufacture which product to maximize total daily product output? (Note: Department 1 does not have the facilities to produce golf clubs.)
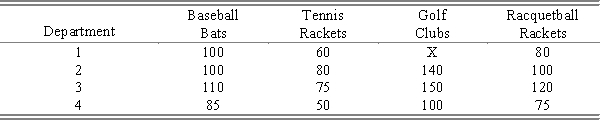
Formulate this assignment problem as a linear program.
Formulate this assignment problem as a linear program.
(Essay)
4.8/5  (41)
(41)
The number of units shipped from origin i to destination j is represented by
(Multiple Choice)
4.9/5  (45)
(45)
The following table shows the unit shipping cost between cities, the supply at each source city, and the demand at each destination city. The Management Scientist solution is shown. Report the optimal solution. 
TRANSPORTATION PROBLEM
*****************************
OBJECTIVE: MINIMIZATION
SUMMARY OF ORIGIN SUPPLIES
********************************
TRANSPORTATION PROBLEM
*****************************
OBJECTIVE: MINIMIZATION
SUMMARY OF ORIGIN SUPPLIES
******************************** 
SUMMARY OF DESTINATION DEMANDS
***************************************
SUMMARY OF DESTINATION DEMANDS
*************************************** 
SUMMARY OF UNIT COST OR REVENUE DATA
*********************************************
SUMMARY OF UNIT COST OR REVENUE DATA
********************************************* 
OPTIMAL TRANSPORTATION SCHEDULE
****************************************
OPTIMAL TRANSPORTATION SCHEDULE
**************************************** 
TOTAL TRANSPORTATION COST OR REVENUE IS 1755
TOTAL TRANSPORTATION COST OR REVENUE IS 1755
(Essay)
4.9/5  (41)
(41)
In the LP formulation of a maximal flow problem, a conservation-of-flow constraint ensures that an arc's flow capacity is not exceeded.
(True/False)
4.9/5  (45)
(45)
The capacitated transportation problem includes constraints which reflect limited capacity on a route.
(True/False)
4.8/5  (33)
(33)
Consider the following shortest-route problem involving seven cities. The distances between the cities are given below. Draw the network model for this problem and formulate the LP for finding the shortest route from City 1 to City 7. 
(Essay)
4.8/5  (46)
(46)
Whenever total supply is less than total demand in a transportation problem, the LP model does not determine how the unsatisfied demand is handled.
(True/False)
4.8/5  (28)
(28)
Showing 21 - 40 of 70
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)