Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution

​Explain the two interpretations of dual prices based on the accounting assumptions made in calculating the objective function coefficients.

Excel's Solver tool has been used in the spreadsheet below to solve a linear programming problem with a maximization objective function and all ≤ constraints. ​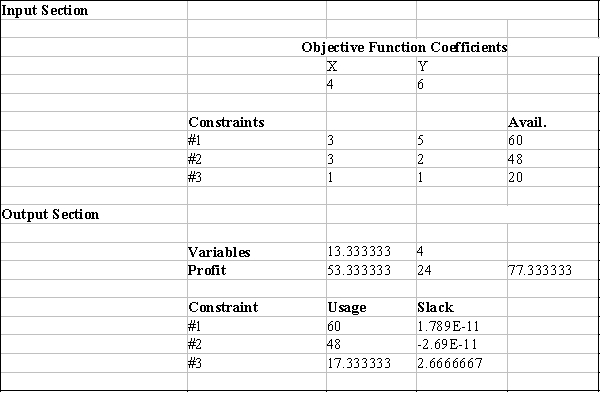 a.Give the original linear programming problem. b.Give the complete optimal solution.

If the optimal value of a decision variable is zero and its reduced cost is zero, this indicates that alternative optimal solutions exist.

Decreasing the objective function coefficient of a variable to its lower limit will create a revised problem that is unbounded.

Use the following Management Scientist output to answer the questions. MIN 4X1+5X2+6X3 S.T. 1) X1+X2+X3<85 2) 3X1+4X2+2X3>280 3) 2X1+4X2+4X3>320 Objective Function Value = 400.000 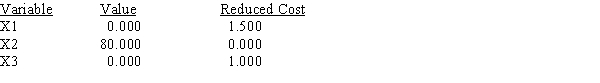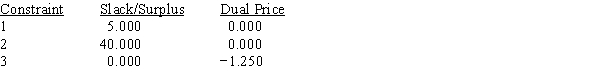OBJECTIVE COEFFICIENT RANGES 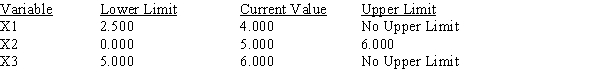RIGHT HAND SIDE RANGES 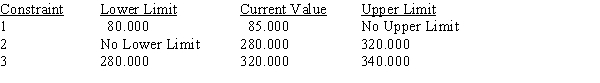a.What is the optimal solution, and what is the value of the profit contribution? b.Which constraints are binding? c.What are the dual prices for each resource? Interpret. d.Compute and interpret the ranges of optimality. e.Compute and interpret the ranges of feasibility.

A section of output from The Management Scientist is shown here. 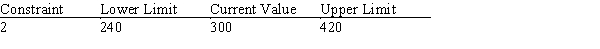What will happen if the right-hand-side for constraint 2 increases by 200?

Excel's Solver tool has been used in the spreadsheet below to solve a linear programming problem with a minimization objective function and all ≥ constraints. ​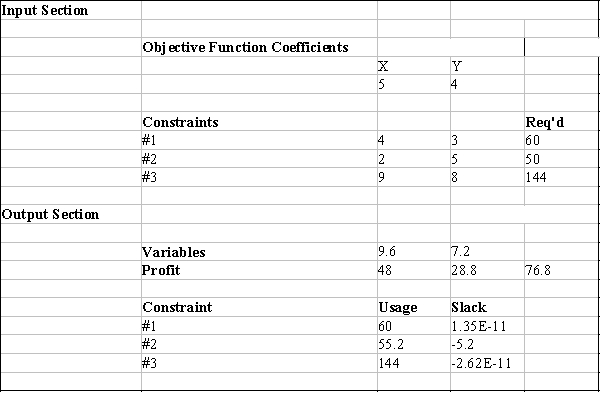 a.Give the original linear programming problem. b.Give the complete optimal solution.

The 100% Rule does not imply that the optimal solution will necessarily change if the percentage exceeds 100%.

LINDO output is given for the following linear programming problem. MIN 12 X1 + 10 X2 + 9 X3 SUBJECT TO 2) 5 X1 + 8 X2 + 5 X3 >= 60 3) 8 X1 + 10 X2 + 5 X3 >= 80 END LP OPTIMUM FOUND AT STEP 1 OBJECTIVE FUNCTION VALUE 1) 80.000000 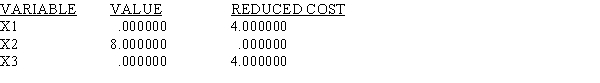NO. ITERATIONS= 1 RANGES IN WHICH THE BASIS IS UNCHANGED: a.What is the solution to the problem? b.Which constraints are binding? c.Interpret the reduced cost for x₁. d.Interpret the dual price for constraint 2. e.What would happen if the cost of x₁ dropped to 10 and the cost of x₂ increased to 12?

The amount of a sunk cost will vary depending on the values of the decision variables.

​Describe each of the sections of output that come from The Management Scientist and how you would use each.

If the range of feasibility indicates that the original amount of a resource, which was 20, can increase by 5, then the amount of the resource can increase to 25.

The binding constraints for this problem are the first and second. Min x₁ + 2x₂ s.t. x₁ + x₂ ≥ 300 2x₁ + x₂ ≥ 400 2x₁ + 5x₂ ≤ 750 x₁ , x₂ ≥ 0 a.Keeping c₂ fixed at 2, over what range can c₁ vary before there is a change in the optimal solution point? b.Keeping c₁ fixed at 1, over what range can c₂ vary before there is a change in the optimal solution point? c.If the objective function becomes Min 1.5x₁ + 2x₂, what will be the optimal values of x₁, x₂, and the objective function? d.If the objective function becomes Min 7x₁ + 6x₂, what constraints will be binding? e.Find the dual price for each constraint in the original problem.

To solve a linear programming problem with thousands of variables and constraints

A negative dual price for a constraint in a minimization problem means

The amount the objective function coefficient of a decision variable would have to improve before that variable would have a positive value in the solution is the

Use the following Management Scientist output to answer the questions. LINEAR PROGRAMMING PROBLEM MAX 31X1+35X2+32X3 S.T. 1) 3X1+5X2+2X3>90 2) 6X1+7X2+8X3<150 3) 5X1+3X2+3X3<120 OPTIMAL SOLUTION Objective Function Value = 763.333 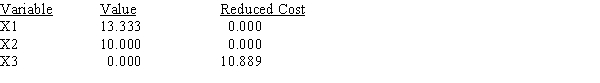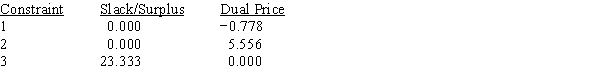OBJECTIVE COEFFICIENT RANGES 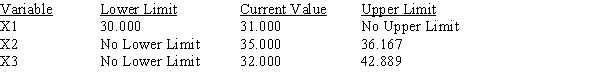RIGHT HAND SIDE RANGES 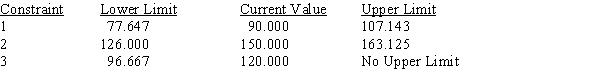a.Give the solution to the problem. b.Which constraints are binding? c.What would happen if the coefficient of x₁ increased by 3? d.What would happen if the right-hand side of constraint 1 increased by 10?

Any change to the objective function coefficient of a variable that is positive in the optimal solution will change the optimal solution.

For a minimization problem, a positive dual price indicates the value of the objective function will increase.

Sensitivity analysis information in computer output is based on the assumption of