Exam 2: An Introduction to Linear Programming
Exam 1: Introduction63 Questions
Exam 2: An Introduction to Linear Programming66 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution56 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management63 Questions
Exam 5: Advanced Linear Programming Applications46 Questions
Exam 6: Distribution and Network Models70 Questions
Exam 7: Integer Linear Programming61 Questions
Exam 8: Nonlinear Optimization Models51 Questions
Exam 9: Project Scheduling: Pertcpm59 Questions
Exam 10: Inventory Models65 Questions
Exam 11: Waiting Line Models68 Questions
Exam 12: Simulation62 Questions
Exam 13: Decision Analysis97 Questions
Exam 14: Multicriteria Decisions50 Questions
Exam 15: Time Series Analysis and Forecasting63 Questions
Exam 16: Markov Processes49 Questions
Exam 17: Linear Programming: Simplex Method51 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality35 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems44 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming38 Questions
Select questions type
A solution that satisfies all the constraints of a linear programming problem except the nonnegativity constraints is called
(Multiple Choice)
4.8/5  (36)
(36)
Explain the steps necessary to put a linear program in standard form.
(Essay)
4.9/5  (42)
(42)
A variable added to the left-hand side of a less-than-or-equal-to constraint to convert the constraint into an equality is
(Multiple Choice)
4.7/5  (30)
(30)
Explain what to look for in problems that are infeasible or unbounded.
(Essay)
5.0/5  (34)
(34)
A linear programming problem can be both unbounded and infeasible.
(True/False)
4.9/5  (34)
(34)
Explain the concepts of proportionality, additivity, and divisibility.
(Essay)
4.9/5  (44)
(44)
For the following linear programming problem, determine the optimal solution by the graphical solution method
Max
−X + 2Y
s.t.
6X − 2Y ≤ 3
−2X + 3Y ≤ 6
X + Y ≤ 3
X, Y ≥ 0
(Essay)
4.9/5  (26)
(26)
Explain the difference between profit and contribution in an objective function. Why is it important for the decision
maker to know which of these the objective function coefficients represent?
(Essay)
4.8/5  (33)
(33)
Because surplus variables represent the amount by which the solution exceeds a minimum target, they are given positive coefficients in the objective function.
(True/False)
4.9/5  (32)
(32)
Increasing the right-hand side of a nonbinding constraint will not cause a change in the optimal solution.
(True/False)
4.8/5  (27)
(27)
An infeasible problem is one in which the objective function can be increased to infinity.
(True/False)
4.9/5  (34)
(34)
The standard form of a linear programming problem will have the same solution as the original problem.
(True/False)
5.0/5  (38)
(38)
Solve the following linear program by the graphical method.
Max
4X + 5Y
s.t.
X + 3Y ≤ 22
−X + Y ≤ 4
Y ≤ 6
2X − 5Y ≤ 0
X, Y ≥ 0
(Essay)
4.7/5  (36)
(36)
A businessman is considering opening a small specialized trucking firm. To make the firm profitable, it is estimated that it must have a daily trucking capacity of at least 84,000 cu. ft. Two types of trucks are appropriate for the specialized operation. Their characteristics and costs are summarized in the table below. Note that truck 2 requires 3 drivers for long haul trips. There are 41 potential drivers available and there are facilities for at most 40 trucks. The businessman's objective is to minimize the total cost outlay for trucks. 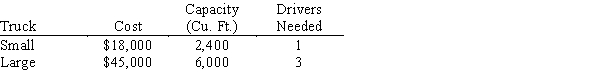
Solve the problem graphically and note there are alternate optimal solutions. Which optimal solution:
a.
uses only one type of truck?
b.
utilizes the minimum total number of trucks?
c.
uses the same number of small and large trucks?
Solve the problem graphically and note there are alternate optimal solutions. Which optimal solution:
a.
uses only one type of truck?
b.
utilizes the minimum total number of trucks?
c.
uses the same number of small and large trucks?
(Essay)
4.7/5  (37)
(37)
In what part(s) of a linear programming formulation would the decision variables be stated?
(Multiple Choice)
4.8/5  (35)
(35)
Create a linear programming problem with two decision variables and three constraints that will include both a slack
and a surplus variable in standard form. Write your problem in standard form.
(Essay)
4.9/5  (35)
(35)
Whenever all the constraints in a linear program are expressed as equalities, the linear program is said to be written in
(Multiple Choice)
4.8/5  (28)
(28)
Showing 21 - 40 of 66
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)