Exam 2: An Introduction to Linear Programming
Exam 1: Introduction63 Questions
Exam 2: An Introduction to Linear Programming66 Questions
Exam 3: Linear Programming: Sensitivity Analysis and Interpretation of Solution56 Questions
Exam 4: Linear Programming Applications in Marketing, Finance, and Operations Management63 Questions
Exam 5: Advanced Linear Programming Applications46 Questions
Exam 6: Distribution and Network Models70 Questions
Exam 7: Integer Linear Programming61 Questions
Exam 8: Nonlinear Optimization Models51 Questions
Exam 9: Project Scheduling: Pertcpm59 Questions
Exam 10: Inventory Models65 Questions
Exam 11: Waiting Line Models68 Questions
Exam 12: Simulation62 Questions
Exam 13: Decision Analysis97 Questions
Exam 14: Multicriteria Decisions50 Questions
Exam 15: Time Series Analysis and Forecasting63 Questions
Exam 16: Markov Processes49 Questions
Exam 17: Linear Programming: Simplex Method51 Questions
Exam 18: Simplex-Based Sensitivity Analysis and Duality35 Questions
Exam 19: Solution Procedures for Transportation and Assignment Problems44 Questions
Exam 20: Minimal Spanning Tree19 Questions
Exam 21: Dynamic Programming38 Questions
Select questions type
Find the complete optimal solution to this linear programming problem.
Max
5X + 3Y
s.t.
2X + 3Y ≤ 30
2X + 5Y ≤ 40
6X − 5Y ≤ 0
X , Y ≥ 0
(Essay)
4.8/5  (29)
(29)
Alternative optimal solutions occur when there is no feasible solution to the problem.
(True/False)
5.0/5  (34)
(34)
Use this graph to answer the questions. 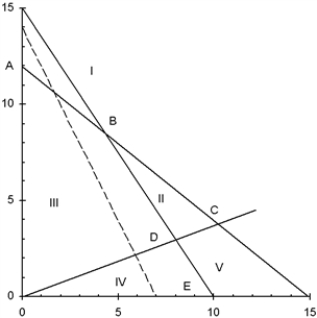 Max
20X + 10Y
s.t.
12X + 15Y ≤ 180
15X + 10Y ≤ 150
3X − 8Y ≤ 0
X , Y ≥ 0
a.Which area (I, II, III, IV, or V) forms the feasible region?
b.Which point (A, B, C, D, or E) is optimal?
c.Which constraints are binding?
d.Which slack variables are zero?
Max
20X + 10Y
s.t.
12X + 15Y ≤ 180
15X + 10Y ≤ 150
3X − 8Y ≤ 0
X , Y ≥ 0
a.Which area (I, II, III, IV, or V) forms the feasible region?
b.Which point (A, B, C, D, or E) is optimal?
c.Which constraints are binding?
d.Which slack variables are zero?
(Essay)
4.9/5  (32)
(32)
Solve the following system of simultaneous equations.
6X + 2Y = 50
2X + 4Y = 20
(Short Answer)
4.9/5  (28)
(28)
Explain the steps of the graphical solution procedure for a minimization problem.
(Essay)
4.9/5  (23)
(23)
In a feasible problem, an equal-to constraint cannot be nonbinding.
(True/False)
4.9/5  (36)
(36)
The three assumptions necessary for a linear programming model to be appropriate include all of the following except
(Multiple Choice)
4.8/5  (39)
(39)
If there is a maximum of 4,000 hours of labor available per month and 300 ping-pong balls (x1) or 125 wiffle balls (x2) can be produced per hour of labor, which of the following constraints reflects this situation?
(Multiple Choice)
4.8/5  (32)
(32)
An unbounded feasible region might not result in an unbounded solution for a minimization or maximization problem.
(True/False)
4.7/5  (37)
(37)
For the following linear programming problem, determine the optimal solution by the graphical solution method. Are any of the constraints redundant? If yes, then identify the constraint that is redundant.
Max
X + 2Y
s.t.
X + Y ≤ 3
X − 2Y ≥ 0
Y ≤ 1
X, Y ≥ 0
(Essay)
4.9/5  (35)
(35)
Infeasibility means that the number of solutions to the linear programming models that satisfies all constraints is
(Multiple Choice)
4.8/5  (35)
(35)
Use a graph to illustrate why a change in an objective function coefficient does not necessarily lead to a change in
the optimal values of the decision variables, but a change in the right-hand sides of a binding constraint does lead to
new values.
(Essay)
5.0/5  (37)
(37)
Given the following linear program:
Min
150X + 210Y
s.t.
3.8X + 1.2Y ≥ 22.8
Y ≥ 6
Y ≤ 15
45X + 30Y = 630
X, Y ≥ 0
Solve the problem graphically. How many extreme points exist for this problem?
(Essay)
4.9/5  (32)
(32)
Find the complete optimal solution to this linear programming problem.
Max
2X + 3Y
s.t.
4X + 9Y ≤ 72
10X + 11Y ≤ 110
17X + 9Y ≤ 153
X , Y ≥ 0
(Essay)
5.0/5  (37)
(37)
Solve the following system of simultaneous equations.
6X + 4Y = 40
2X + 3Y = 20
(Short Answer)
4.9/5  (41)
(41)
Solve the following linear program graphically.
Max
5X + 7Y
s.t.
X ≤ 6
2X + 3Y ≤ 19
X + Y ≤ 8
X, Y ≥ 0
(Essay)
5.0/5  (28)
(28)
Showing 41 - 60 of 66
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)